Table of Contents¶
Algorithme génétique pour générer des éclairages - texte de modélisation agrég¶
Préparation à l'agrégation - ENS de Rennes, 2018-19¶
- Date : 12 mars 2019
- Auteur : Lilian Besson
- Texte: Annale 2012, "Éclairage graphe" (public2012-D1)
À propos de ce document¶
- Ceci est une proposition de correction, partielle et probablement non-optimale, pour la partie implémentation d'un texte d'annale de l'agrégation de mathématiques, option informatique.
- Ce document est un notebook Jupyter, et est open-source sous Licence MIT sur GitHub, comme les autres solutions de textes de modélisation que j'ai écrite cette année.
- L'implémentation sera faite en Python 3.
Graphes, éclairages et structures de données¶
On donne tout de suite un exemple de graphe, en prenant le 3ème exemple de la Figure 1 du texte.
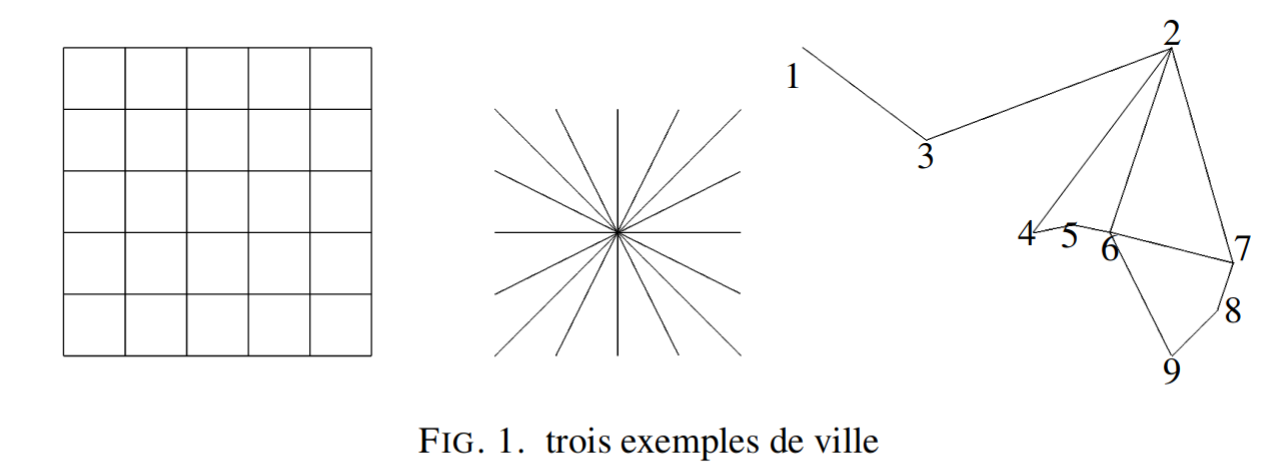
On va définir ce graphe, comme une liste d'arêtes, et plusieurs éclairages.
In [13]:
graphe1 = [(1,3), (3,2), (2,4), (2,6), (2,7), (4,5), (5,6), (6,7), (6,9), (7,8), (8,9)]
graphe1 = [ (u-1, v-1) for (u,v) in graphe1 ]
In [14]:
def nbsommets(graphe):
n = 0
for (u, v) in graphe:
if u > n or v > n: n = max(u, v)
return n + 1
In [15]:
nbsommets(graphe1)
Out[15]:
Quatre exemples d'éclairages, deux satisfaisant donc l'un trivialement, et les deux autres non satisfaisants :
In [16]:
eclairage1_sat = [0, 1, 2, 3, 4, 5, 6, 7, 8] # trivialement valide car on éclaire tout
eclairage2_sat = [1, 2, 3, 5, 6, 8] # valide mais on éclaire pas tout
In [17]:
eclairage1_nonsat = [2, 4, 8]
eclairage2_nonsat = [1, 2, 3, 5, 6]
Fonctions nécessaires pour l'algorithme génétique¶
On va devoir implémenter des fonctions réalisants les tâches suivantes :
- vérifier qu'un ensemble de sommets éclairés est un éclairage valide,
- vérifier qu'un éclairage donné sous forme de tableau de
gauche,droite,lesdeuxest un éclairage valide, - compter le nombre de places éclairés pour un éclairage donné sous la forme précédente (c'est la fonction de coût, ou "fitness" de l'algorithme génétique).
Ensuite pour l'initialisation de l'algorithm génétique il nous faudra :
- générer un éclairage aléatoirement,
- faire ça 100 fois pour avoir une population initiale.
Et puis pour chaque étape de l'algorithme génétique, on transformera les 100 individus
- trier une population d'éclairages suivant un critère (= le nombre de lampadaires utilisés),
- faire muter aléatoirement 4 éclairages parmi les 48 meilleurs,
- se faire reproduire les 48 moins bons individus restants par "crossing over", ou mutation croisée.
Validité d'un éclairage¶
In [22]:
def est_eclairage(graphe, places_eclairees):
""" Cette fonction est en O(M + L) = O(M) où M est le nombre d'arêtes, et L le nombre de places éclairées (<= N <= M par connexité).
"""
n = nbsommets(graphe)
sont_eclairees = [ False for _ in range(n) ]
for p in places_eclairees:
sont_eclairees[p] = True
for (u, v) in graphe:
if not sont_eclairees[u] and not sont_eclairees[v]:
return False
return True
In [23]:
est_eclairage(graphe1, eclairage1_sat)
Out[23]:
In [24]:
est_eclairage(graphe1, eclairage2_sat)
Out[24]:
In [25]:
est_eclairage(graphe1, eclairage1_nonsat)
Out[25]:
In [26]:
est_eclairage(graphe1, eclairage2_nonsat)
Out[26]:
Minimalité d'un éclairage¶
In [35]:
def places_moins_une(places_eclairees, place_a_enlever):
""" En O(L) si L est le nombre de places éclairées."""
return [place for place in places_eclairees if place != place_a_enlever]
def est_minimal(graphe, places_eclairees):
""" Cette fonction est en O(M L) où M est le nombre d'arêtes, et L le nombre de places éclairées.
"""
return est_eclairage(graphe, places_eclairees) and not(all([
est_eclairage(graphe, places_moins_une(places_eclairees, place_a_enlever))
for place_a_enlever in places_eclairees
]))
In [36]:
est_minimal(graphe1, eclairage1_sat)
Out[36]:
In [37]:
est_minimal(graphe1, eclairage2_sat)
Out[37]:
In [38]:
est_minimal(graphe1, eclairage1_nonsat)
Out[38]:
In [39]:
est_minimal(graphe1, eclairage2_nonsat)
Out[39]:
Conversion entre liste de valeurs ternaires et éclairage¶
Si le graphe $G=(V,E)$ est donné par un tableau de ses rues $E = \{(u,v)\}$, on représente une liste de places éclairées $V'$ par un tableau de valeurs ternaires gauche, droite ou lesdeux.
In [83]:
gauche, droite, lesdeux = "G", "D", "2"
In [84]:
def eclairage_vers_ternaires(graphe, places_eclairees):
""" O(M)"""
n = nbsommets(graphe)
ternaires = []
sont_eclairees = [ False for _ in range(n) ]
for p in places_eclairees:
sont_eclairees[p] = True
for (u,v) in graphe:
if sont_eclairees[u] and sont_eclairees[v]:
ternaires.append(lesdeux)
elif sont_eclairees[u]:
ternaires.append(gauche)
elif sont_eclairees[v]:
ternaires.append(droite)
return ternaires
In [85]:
def ternaires_vers_eclairage(graphe, ternaires):
""" O(M)"""
n = nbsommets(graphe)
places_eclairees = [ False for _ in range(n) ]
for (u,v), ternaire in zip(graphe, ternaires):
if ternaire == gauche or ternaire == lesdeux:
places_eclairees[u] = True
if ternaire == droite or ternaire == lesdeux:
places_eclairees[v] = True
# O(N)
eclairage = []
for i, p in enumerate(places_eclairees):
if p: eclairage.append(i)
return eclairage
In [94]:
def est_valide_ternaires(graphe, ternaires):
""" O(M)"""
return est_eclairage(graphe, ternaires_vers_eclairage(graphe, ternaires))
In [87]:
graphe1
Out[87]:
In [139]:
ternaires1_sat = eclairage_vers_ternaires(graphe1, eclairage1_sat)
ternaires1_sat
Out[139]:
In [89]:
print(eclairage1_sat)
ternaires_vers_eclairage(graphe1, eclairage_vers_ternaires(graphe1, eclairage1_sat))
Out[89]:
In [141]:
ternaires2_sat = eclairage_vers_ternaires(graphe1, eclairage2_sat)
ternaires2_sat
Out[141]:
In [95]:
print(eclairage2_sat)
print(eclairage_vers_ternaires(graphe1, eclairage2_sat))
print(ternaires_vers_eclairage(graphe1, eclairage_vers_ternaires(graphe1, eclairage2_sat)))
print(est_valide_ternaires(graphe1, eclairage_vers_ternaires(graphe1, eclairage2_sat)))
Fonction de coût¶
On a donc la "fonction de coût" recherchée :
In [106]:
def nb_places_eclairees(graphe, ternaires):
""" O(M)"""
eclairage = ternaires_vers_eclairage(graphe, ternaires)
return len(eclairage)
Génération aléatoire d'un individu¶
In [150]:
import random
def un_ternaire_aleatoire():
""" O(1)"""
return random.choice([gauche, droite, lesdeux])
def un_ternaire_aleatoire_different(valeur):
""" O(1)"""
if valeur == gauche:
return random.choice([droite, lesdeux])
elif valeur == droite:
return random.choice([gauche, lesdeux])
else:
return random.choice([gauche, droite])
def un_individu(graphe):
""" O(M)"""
return [un_ternaire_aleatoire() for (u,v) in graphe]
On peut facilement générer dix individus différents, qui sont tous des éclairages valides, et afficher leur coût :
In [108]:
for _ in range(10):
ternaires = un_individu(graphe1)
assert est_valide_ternaires(graphe1, ternaires)
cout = nb_places_eclairees(graphe1, ternaires)
print("L'éclairage", ternaires, "a un coût =", cout)
Génération aléatoire d'une population¶
In [110]:
def population_initiale(graphe, taille_population):
return [ un_individu(graphe) for _ in range(taille_population) ]
Par exemple, une population initiale de taille 5 est :
In [129]:
pop = population_initiale(graphe1, 5)
for individu in pop:
print("L'éclairage", individu, "a un coût =", nb_places_eclairees(graphe1, individu))
In [130]:
sorted(pop, key=lambda individu: nb_places_eclairees(graphe1, individu))
Out[130]:
On peut donc facilement trier des
Squelette générique pour l'algorithme génétique¶
On va écrire une fonction générique. Pour visualiser l'évolution de la population, plutôt que d'afficher une liste de 100 coûts, je préfère afficher un décompte du nombre d'individus ayant un certain coût, en Python cela se fait très facilement avec collections.Counter :
In [192]:
import collections
collections.Counter([1,1,1,1,1,2,2,2,3])
Out[192]:
In [193]:
def algorithme_genetique(
pop_init,
fct_cout,
muter_un,
croiser_deux,
taille_pop=100,
tau_meilleurs=0.48,
tau_cross=0.48,
nb_generations=1000,
):
""" Complexité en O(nb_generations * [
taille_pop * log(taille_pop) * C_cout
+ taille_pop * C_croisement
+ taille_pop * C_mutation
) où :
- C_cout est le coût de calcul de la fonction d'évaluation fct_cout,
- C_croisement est le coût de calcul de la fonction de croisement croiser_deux,
- C_mutation est le coût de calcul de la fonction de mutation muter_un,
"""
nb_meilleurs = int(tau_meilleurs * taille_pop)
nb_enfants = 2 * (int(tau_cross * taille_pop)//2) # nb paire !
nb_mutes = taille_pop - nb_meilleurs - nb_enfants
# première population
pop = pop_init(taille_pop)
# nb_generations étapes, toutes identiques
for generation in range(nb_generations):
couts = [fct_cout(sol) for sol in pop]
# bonus: affichage de la liste des couts
print("La génération numéro", generation, "a les coûts suivants :", collections.Counter(couts))
pop_triees = sorted(pop, key=fct_cout)
# 1) on prend les 48% meilleurs, laissés tels quels
meilleurs = pop_triees[:nb_meilleurs]
# 2) on prend les 48% moins bons, on les croise
moins_bons = pop_triees[-nb_enfants:]
enfants = [ ]
for i in range(len(moins_bons) // 2):
parent_1 = moins_bons[2*i]
parent_2 = moins_bons[2*i + 1]
enfant_1, enfant_2 = croiser_deux(parent_1, parent_2)
enfants.append(enfant_1)
enfants.append(enfant_2)
# 3) on prend les 4% meilleurs, et on les mute un peu
mutes = [ ]
for i in range(nb_mutes):
sain = meilleurs[i]
un_xmen = muter_un(sain)
mutes.append(un_xmen)
# on combine les trois listes en une nouvelle population
nouvelle_pop = meilleurs + enfants + mutes
pop = nouvelle_pop
# a la fin, on renvoie la meilleure solution
meilleure_solution = max(pop, key=fct_cout)
return meilleure_solution
Mutations et croisements¶
On doit encore écrire les deux fonctions clés, muter_un et croiser_deux.
In [180]:
def une_mutation(graphe, ternaires):
position = random.randint(0, len(ternaires) - 1)
mute = [ t for t in ternaires ]
mute[position] = un_ternaire_aleatoire_different(mute[position])
return mute
def mutation(graphe, ternaires):
M = len(graphe)
nb_mutation = random.randint(1, M)
mute = une_mutation(graphe, ternaires)
for _ in range(nb_mutation - 1):
mute = une_mutation(graphe, mute)
return mute
In [181]:
graphe1
ternaires1_sat
Out[181]:
Out[181]:
In [182]:
une_mutation(graphe1, ternaires1_sat)
Out[182]:
In [183]:
mutation(graphe1, ternaires1_sat)
Out[183]:
In [184]:
mutation(graphe1, ternaires1_sat)
Out[184]:
In [185]:
mutation(graphe1, ternaires1_sat)
Out[185]:
In [186]:
def croiser_deux_ternaires(graphe, ternaires_1, ternaires_2):
M1 = len(ternaires_1) // 2
M2 = len(ternaires_2) // 2
enfant_1 = ternaires_1[:M1] + ternaires_2[M2:]
enfant_2 = ternaires_1[M1:] + ternaires_2[:M2]
return enfant_1, enfant_2
In [187]:
print("Les deux parents suivants :")
ternaires_1 = mutation(graphe1, ternaires1_sat)
print(ternaires_1)
ternaires_2 = mutation(graphe1, ternaires1_sat)
print(ternaires_2)
enfant_1, enfant_2 = croiser_deux_ternaires(graphe1, ternaires_1, ternaires_2)
print("peuvent par exemple donner les deux enfants suivants :")
print(enfant_1)
print(enfant_2)
Génération d'éclairage par algorithme génétique¶
On assemble le tout :
In [194]:
def eclairage_genetique(graphe,
taille_pop=100,
tau_meilleurs=0.48,
tau_cross=0.48,
nb_generations=50,
):
""" Complexité en O(nb_generations * [
taille_pop * log(taille_pop) * O(M)
+ taille_pop * O(M)
+ taille_pop * O(M)
) = O (nb_generations * taille_pop * log(taille_pop) * M) où :
- M est le nombre d'arêtes dans le graphe.
Donc si nb_generations et taille_pop sont constantes, cette fonction est en O(M).
"""
# on définit les quatre fonctions, pour ce graphe
def pop_init(taille_pop):
return population_initiale(graphe, taille_pop)
def fct_cout(individu):
return nb_places_eclairees(graphe, individu)
def muter_un(individu):
return mutation(graphe, individu)
def croiser_deux(parent_1, parent_2):
return croiser_deux_ternaires(graphe, parent_1, parent_2)
# on appelle la fonction générique
return algorithme_genetique(
pop_init,
fct_cout,
muter_un,
croiser_deux,
taille_pop=taille_pop,
tau_meilleurs=tau_meilleurs,
tau_cross=tau_cross,
nb_generations=nb_generations,
)
Et on donne un exemple :
In [205]:
eclairage_genetique(graphe1)
Out[205]:
On a trouvé un éclairage valide avec seulement 5 places éclairées, en partant d'une population qui avait des coûts entre 7 et 9.
Conclusion¶
Si vous êtes curieux, je vous laisse travailler davantage sur ça.