Table of Contents¶
Texte d'oral de modélisation - Agrégation Option Informatique¶
Préparation à l'agrégation - ENS de Rennes, 2016-17¶
- Date : 22 mai 2017
- Auteur : Lilian Besson
- Texte: Annale 2010, "Tissus cellulaires" (public2010-D2)
À propos de ce document¶
- Ceci est une proposition de correction, partielle et probablement non-optimale, pour la partie implémentation d'un texte d'annale de l'agrégation de mathématiques, option informatique.
- Ce document est un notebook Jupyter, et est open-source sous Licence MIT sur GitHub, comme les autres solutions de textes de modélisation que j'ai écrite cette année.
- L'implémentation sera faite en OCaml, version 4+ :
Sys.command "ocaml -version";;
Question de programmation¶
La question de programmation pour ce texte était donnée au tout début, et occupe toute la page 2 :
Modélisation¶
On veut simuler un phénomène de contamination. L’état d’une cellule est représenté par un entier compris entre $0$ et $K$ ($K \geq 1$ est un paramètre fixé).
Une cellule est normalement saine, non contaminée, dans l’état $0$ et reste dans cet état tant qu’elle n’est pas infectée. Tous les autres états représentent différents stades d’infection. Une cellule infectée commence dans l’état $1$ et à chaque itération passe dans l’état suivant (c.-à-d. $2$ puis $3$ puis...). Quand elle atteint l’état $K$, elle a remporté sa lutte contre l’infection et retourne à l’état $0$, saine et non infectée à l’itération suivante.
Une cellule infectée n’est pas tout de suite contagieuse (c.-à-d. capable d’infecter ses voisines). Une cellule devient infectieuse à partir du stade $I$ ($I \leq K$, $I$ est un autre paramètre fixé) et le reste jusqu’à sa guérison (retour à l’état $0$). Durant cette période, elle peut contaminer chacune de ses deux voisines (les plus proches à droite et à gauche). Si celles-ci ne sont pas déjà infectées, elles le deviennent automatiquement, au stade $1$; si elles sont déjà infectées, elles le restent.
Les cellules ne bougent pas et on les suppose rangées les unes à côté des autres sur une ligne. Elles sont toutes mises à jour en même temps, de manière synchrone. Pour simplifier, on suppose que les première et dernière cellules restent toujours dans le même état $0$.
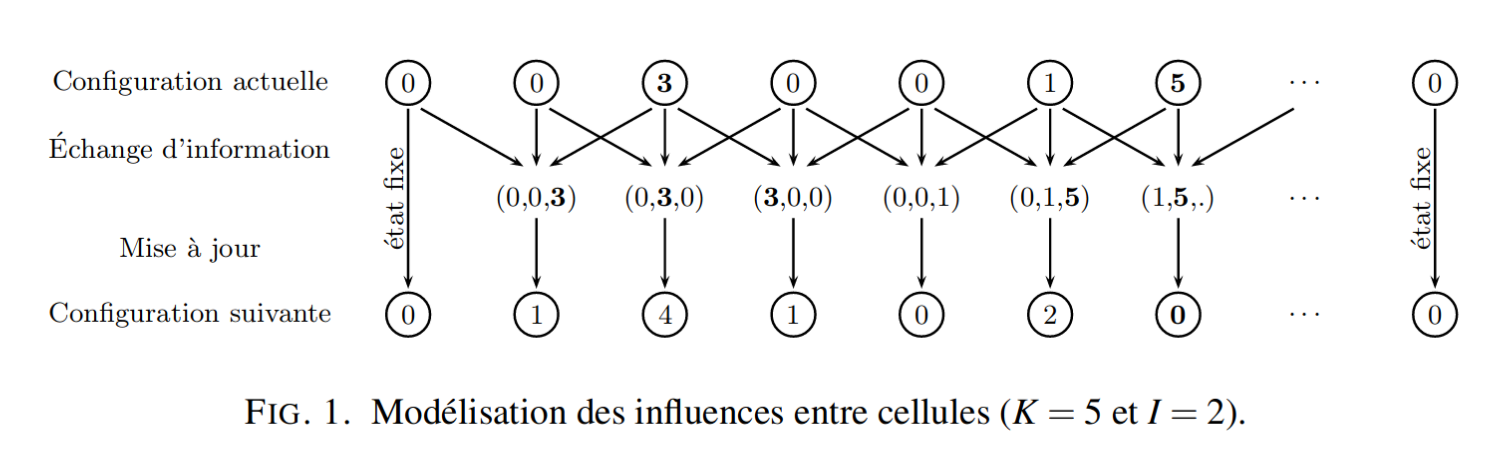
Tout ceci est schématisé sur la Fig. 1 où l’on voit en haut une configuration et en bas la configuration suivante. Chaque cellule est mise à jour en fonction de ses deux plus proches voisines, sauf pour les cellules des deux extrémités dont l’état ne change pas. Après la configuration $(0, 0, 3, 0, 0, 1, 5 ,\dots, 0 )$, le système passe donc à la configuration $(0, 1, 4, 1, 0, 2, 0 ,\dots, 0 )$ pour $K = 5$ et $I = 2$. Dans cette illustration, l’état de la troisième cellule (3) est en gras pour indiquer pour quelles cellules il intervient durant la mise à jour.
Exercice¶
Écrire un programme permettant d’afficher la progression de la contamination sur une vingtaine d’itérations, par exemple pour les valeurs ($K = 5$ et $I = 2$) en partant d’une seule cellule infectée sur une ligne d’une vingtaine de cellules saines.
Préciser la complexité en temps et en espace de la simulation.
Solution¶
On va essayer d'être rapide et de faire simple, aussi $K=5$ et $I=2$ seront fixés et constants dans tout le code suivant.
Les constantes $K$ et $I$ de la simulation sont fixées :
- $K = 5$ fixe le nombre d'états différents dans lequel peut être une cellule,
- $I = 2$ fixe le seuil à partir duquel une cellule devient contagieuse
let k = 5;;
let i = 2;;
assert (i <= k);;
Pour une cellule¶
L'état d'une cellule est un entier :
type etatcellule = int;;
Voici quelques fonctions "triviales" pour traduire les propriétés décrites par le texte :
(** Une cellule est saine si son état est [0], infectée sinon. *)
let est_saine (etat : etatcellule) : bool =
etat = 0
;;
let grossir (etat : etatcellule) : etatcellule =
if etat >= k then 0 else (etat + 1)
;;
let est_contagieuse (etat : etatcellule) : bool =
etat >= i
;;
let infecte (etat : etatcellule) : etatcellule =
if etat = 0 then 1 else etat
;;
Pour une ligne de cellule (un tissu)¶
Si on voulait représenter des tissus en plusieurs dimensions (2, 3),
ici on devrait utiliser etatcellule array array (ou etatcellule array array array),
mais en 1D, etatcellule array suffit.
type tissu = etatcellule array;;
Pour créer un nouvel organse, constitué uniquement de cellules saines :
let nouveau_tissu (length : int) : tissu =
Array.make length (0 : etatcellule)
;;
Par exemple, un "muscle", long de 20 cellules, toutes saines :
let muscle1 : tissu = nouveau_tissu 20;;
Cette fonction sera un raccourci utile pour infecter une cellule choisie :
let infecte_cible (org : tissu) (indice : int) : unit =
org.(indice) <- (infecte org.(indice))
;;
Un second muscle, long de 21 cellules, avec une seule cellule malade en indice 11 :
let muscle2 : tissu =
let m = nouveau_tissu 21 in begin
infecte_cible m 11;
m
end
;;
- Toutes ces fonctions s'exécutent en temps constant $\mathcal{O}(1)$.
Évolution d'une cellule qui n'est pas au bord en fonction de l'état précédent de ces deux voisins et de son état.¶
On représente une cellule avec ses deux voisins :
type lcor = { l : etatcellule; co : etatcellule; r : etatcellule; };;
On peut ensuite donner l'état de la cellule courante (précédemment dans l'état co) en fonction de l'état de sa voisine de gauche l et de droite r :
let nouvel_etat_cellule ({l; co; r} : lcor) () : etatcellule =
if co = k then
(* La cellule guérit, ce qu'on autoriserait plus dans le second modèle. *)
0
else begin
if (est_saine co) then
(* Si elle est saine, elle peut devenir infectée : *)
if ( (est_contagieuse l) || (est_contagieuse r) )
then
(* Devient infectée. *)
1
else
co
else
(* Si elle est déjà infectée, elle grandit toute seule. *)
grossir co
end
;;
- Cette fonction s'exécute en temps constant $\mathcal{O}(1)$.
Construction du sous-tableau des triplets lcor, en ignorant la première et dernière cellule :
let cree_lcor (org : tissu) : lcor array =
let n = Array.length org in
assert (n >= 2);
Array.init (n - 2) (fun i ->
{ l = org.(i); co = org.(i + 1); r = org.(i + 2) }
)
;;
- Cette fonction s'exécute en temps linéaire $\mathcal{O}(n)$.
Testons sur les deux exemples précédents :
let lcor1 = cree_lcor muscle1;;
let lcor2 = cree_lcor muscle2;;
Un troisième exemple plus intéressant sera le tissu de la Figure 1, qu'on supposera de petite taille.
let muscle3 = [| 0; 0; 3; 0; 0; 1; 5; 0; 0 |];;
let lcor3 = cree_lcor muscle3;;
Une fonction concise pour afficher un tissu (ie. une ligne de cellules)¶
let print = Format.printf;;
let print_tissu_x (etats : etatcellule list) : unit =
match etats with
| [] -> print "";
| s0 :: [] -> print "[ %i ]" s0;
| s0 :: l -> begin
print "[ %i" s0;
List.iter (fun (s : etatcellule) -> print "-%i" s) l;
print " ]";
end
;;
- Cette fonction s'exécute en temps linéaire $\mathcal{O}(n)$.
Simple fonction pour afficher un tissu (revient à afficher un tableau) :
let print_tissu (o : tissu) : unit =
print_tissu_x (Array.to_list o)
;;
print_tissu muscle1;;
print_endline " : muscle 1.\n";;
flush_all ();;
print_tissu muscle2;;
print_endline " : muscle 2.\n";;
flush_all ();;
print_tissu muscle3;;
print_endline " : muscle 3.\n";;
flush_all ();;
La fonction demandée pour faire évoluer un tissu, étape par étape.¶
Attention, elle agit par effet de bords ! (i.e., en modifiant en place le tissu donné, c'est pour ça qu'on utilise des tableaux et non des listes).
Cette fonction renvoie la valeur du tissu, pour éventuellement faire des sauvegardes ou l'afficher, mais le tissu est bien modifié en place !
let une_etape_infection (ti : tissu) : tissu =
let n = Array.length ti in
let lcor_ti = cree_lcor ti in
for j = 1 to n - 2 do
ti.(j) <- nouvel_etat_cellule lcor_ti.(j-1) ()
done;
ti
;;
- Cette fonction s'exécute en temps linéaire $\mathcal{O}(n)$, puisque
cree_lcorl'est, etnouvel_etat_celluleest en temps constant.
Un exemple sur le tissu sain, le tissu infecté au milieu et le tissu de la Figure 1.
une_etape_infection muscle1;;
une_etape_infection muscle2;;
une_etape_infection muscle3;;
Faire évoluer sur plusieurs étapes, en affichant les étapes intermédiaires¶
let m_etapes_infection (ti : tissu) (m : int) : tissu =
print "\n\nSTART : %i étapes de propagation de l'infection." m;
print "\nÉtape 0 : ";
print_tissu ti;
for j = 1 to m do
print "\nÉtape %.2i : " j;
print_tissu (une_etape_infection ti);
done;
flush_all ();
ti
;;
- Cette fonction s'exécute en temps $\mathcal{O}(n \times m)$, puisqu'elle appelle $m$ fois
une_etape_infectionqui est en temps linéaire $\mathcal{O}(n)$.
On relance les exemples depuis le début :
let muscle1 = nouveau_tissu 20;;
m_etapes_infection muscle1 3;;
(* Il n'évolue pas *)
let muscle2 = let m = nouveau_tissu 21 in begin infecte_cible m 11; m end;;
m_etapes_infection muscle2 40;;
(* tout le tissu est infecté ! Dès la 20ème étape *)
let muscle3 = [| 0; 0; 3; 0; 0; 1; 5; 0; 0 |];;
m_etapes_infection muscle3 8;;
(* 3 étapes suffisent à tout infecter *)
Voilà, ce sera tout pour cette solution.
Complexités en temps et espace (bonus)¶
Il est toujours utile de préciser, rapidement à l'oral et/ou dans le code (un commentaire suffit) les complexité (ou ordre de grandeur) des fonctions exigées par l'énoncé.
En temps¶
- Une étape d'infection, i.e.,
une_etape_infection, est en temps linéaire $\mathcal{O}(n)$ (et c'est optimal), - Donc $m$ étapes, i.e.,
m_etapes_infection, est en temps $\mathcal{O}(n \times m)$ (et c'est optimal).
En espace¶
Tout est bien évidemment linéaire en $n$ la taille du tissu.
Conclusion¶
Voilà pour la question obligatoire de programmation.
Qualités¶
- On a décomposé le problème en sous-fonctions,
- on a fait des exemples et on les garde dans ce qu'on présente au jury,
- on a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte).
Défauts¶
- Par contre, on a testé avec uniquement une valeur pour $I$ et $K$ (resp., $2$ et $5$), et les fonctions écrites ne sont pas paramétriques en $I$ et $K$. (notez que ce serait assez trivial de les rendre des paramètres)
Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive.
Vous auriez pu choisir de modéliser le problème avec une autre approche, ou vous auriez pu expérimenter des extensions de cette approche (e.g., des tissus en 2D ou 3D).