Table of Contents¶
Texte d'oral de modélisation - Agrégation Option Informatique¶
Préparation à l'agrégation - ENS de Rennes, 2017-18¶
- Date : 6 décembre 2017
- Auteur : Lilian Besson
- Texte: Annale 2018, "Expressions arithmétiques" (public2018-D1)
À propos de ce document¶
- Ceci est une proposition de correction, partielle et probablement non-optimale, pour la partie implémentation d'un texte d'annale de l'agrégation de mathématiques, option informatique.
- Ce document est un notebook Jupyter, et est open-source sous Licence MIT sur GitHub, comme les autres solutions de textes de modélisation que j'ai écrite cette année.
- L'implémentation sera faite en OCaml, version 4+ :
Sys.command "ocaml -version";;
print_endline Sys.ocaml_version;;
Question de programmation¶
La question de programmation pour ce texte était donnée en fin de page 6 :
Modélisation¶
On est libre de choisir l'implémentation qui nous convient pour les expressions arithmétiques sous forme arborescente.
Je choisis de ne considérer que les variables et pas les valeurs (on aura des expressions en OCaml comme F("x") pour la variable $x$), et uniquement des arbres binaires.
Les noeuds N(t1, op, t2) sont étiquetées par un opérateur binaire op, dont on fournit à l'avance une liste fixée et finie, et les feuilles F(s) sont étiquetées par une variable s.
Exercice¶
« Écrire une fonction qui reçoit en argument une expression algébrique donnée sous forme arborescente et décore cette expression en calculant pour chaque nœud interne quelle est la valeur du paramètre ρ et quelle branche doit être évaluée en premier selon l’algorithme d’Ershov. »
Solution¶
On va essayer d'être rapide et de faire simple, donc on choisit une algèbre de termes particulière, mais l'algorithme d'Ershov sera implémenté de façon générique (polymorphique, peu importe la valeur de op).
Types et représentations¶
type operateur = Plus | Moins | MoinsDroite | Mul | Div | DivDroite | Modulo | Expo ;;
(* On utilisera MoinsDroite et DivDroite pour la compilation avec la méthode d'Ershov *)
type ('a, 'b) arbre_binaire = N of (('a,'b) arbre_binaire) * 'b * (('a,'b) arbre_binaire) | F of 'a
Par exemple pour l'expression $\frac{x - yz}{u - vw}$, c'est-à-dire (x - y*z)/(u - v*w) :
(* exp1 = (x - y*z) *)
let exp1 =
N(
F("x"),
Moins,
N(
F("y"),
Mul,
F("z")
)
)
;;
(* exp2 = (u - v*w) *)
let exp2 =
N(
F("u"),
Moins,
N(
F("v"),
Mul,
F("w")
)
)
;;
(* exp3 = (x - y*z)/(u - v*w) *)
let exp3 =
N(
exp1,
Div,
exp2
)
Calcul récursif du nombre $\rho$¶
C'est assez immédiat, en suivant la définition récursive : $\rho(F) = 0$ et $\rho(N(t_1, t_2)) = \rho(t_1) + 1$ si $\rho(t_1) = \rho(t_2)$ et $\max(\rho(t_1), \rho(t_2))$ si $\rho(t_1) \neq \rho(t_2)$.
let rec nombre_rho (expr : ('a, 'b) arbre_binaire) : int =
match expr with
| F _ -> 0
| N(t1, _, t2) ->
let d1, d2 = nombre_rho t1, nombre_rho t2 in
if d1 = d2 then
d1 + 1
else
max d1 d2
;;
Pour comparer avec le calcul, plus simple, de la hauteur de l'arbre :
let rec hauteur (expr : ('a, 'b) arbre_binaire) : int =
match expr with
| F _ -> 0
| N(t1, _, t2) ->
let d1, d2 = hauteur t1, hauteur t2 in
1 + (max d1 d2)
;;
Exemples qui concordent avec le texte :
let _ = hauteur exp1;;
let _ = nombre_rho exp1;;
let _ = hauteur exp2;;
let _ = nombre_rho exp2;;
let _ = hauteur exp3;;
let _ = nombre_rho exp3;;
Algorithme demandé pour décorer l'arbre¶
On choisit d'ajouter une décoration de type 'c :
type ('a, 'b, 'c) arbre_binaire_decore = N2 of ('c * (('a, 'b, 'c) arbre_binaire_decore) * 'b * (('a, 'b, 'c) arbre_binaire_decore)) | F2 of 'a
On a besoin d'attacher à chaque noeud son paramètre $\rho$ et un drapeau binaire permettant de savoir si l'algorithme d'Ershov indique d'évaluer en premier le sous-arbre gauche (premier_gauche = true) ou droite (= false).
type decoration = {
rho : int;
premier_gauche : bool;
};;
let rec decore (expr : (('a, 'b) arbre_binaire)) : (('a, 'b, decoration) arbre_binaire_decore) =
match expr with
| F v -> F2 v
| N (t1, o, t2) ->
let d1, d2 = nombre_rho t1, nombre_rho t2 in
let d = if d1 = d2 then d1 + 1 else max d1 d2 in
N2({rho = d; premier_gauche = (d2<= d1)}, (decore t1), o, (decore t2))
;;
Dans nos exemples, on voit que l'évaluation favorise en premier (avec des premier_gauche = false) les expressions les plus profondes (à droite) au sens du paramètre $\rho$ :
decore exp1;;
decore exp2;;
decore exp3;;
Complexités¶
En espace¶
Les deux fonctions présentées ci-dessus n'utilisent pas d'autre espace que l'arbre décoré, et la pile d'appel récursif.
- Le calcul récursif de $\rho(t)$ prend donc un espace proportionnel au nombre d'appel récursif imbriqué, qui est borné par la taille du terme $t$ (définie comme le nombre de noeuds et de feuilles), donc est linéaire,
- Le calcul de la méthode d'Ershov est elle aussi linéaire puisque l'arbre décoré est de même taille que l'arbre initial.
En temps¶
Les deux fonctions présentées ci-dessus sont linéaires dans la taille de l'arbre.
Implémentations supplémentaires¶
On peut essayer d'implémenter une fonction qui afficherait ceci pour la méthode d'évaluation naturelle :

Et ceci pour la méthode d'Ershov :
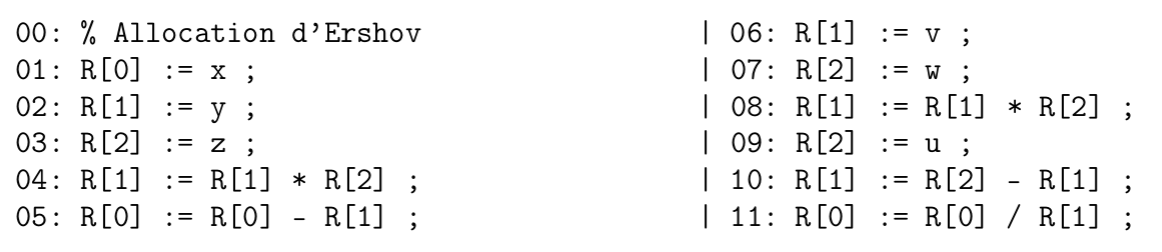
Ce n'est pas trop difficile, mais ça prend un peu de temps :
- on va d'abord montrer comment évaluer les expressions, en lisant l'arbre et en effectuant des appels récursifs,
- puis on fera un parcours postfix de l'arbre afin d'utiliser l'évaluation avec une pile, avec la stratégie naïve,
- et enfin la méthode d'Ershov permettra de réduire la hauteur maximale de la pile, en passant de $h(t)$ (hauteur de l'arbre) à $\rho(t)$,
- en bonus, on affichera les instructions style "compilateur à registre", pour visualiser le gain apporté par la méthode d'Ershov.
Bien sûr, tout cela fait beaucoup trop pour être envisagé le jour de l'oral ! Mais un des points aurait pû être implémenté rapidement.
Évaluation des expressions¶
Un premier objectif plus simple est d'évaluer les expressions, en fournissant un contexte (table associant une valeur à chaque variable).
type ('a, 'b) contexte = ('a * 'b) list;;
let valeur (ctx : ('a, 'b) contexte) (var : 'a) = List.assoc var ctx;;
(* une Hashtbl peut etre utilisee si besoin de bonnes performances *)
let contexte1 : (string, int) contexte = [
("x", 1); ("y", 2); ("z", 3);
("u", 4); ("v", 5); ("w", 6)
];;
let intop_of_op (op : operateur) : (int -> int -> int) =
match op with
| Plus -> ( + )
| Moins -> ( - )
| MoinsDroite -> (fun v1 -> fun v2 -> v2 - v1)
| Mul -> ( * )
| Div -> ( / )
| DivDroite -> (fun v1 -> fun v2 -> v2 / v1)
| Modulo -> ( mod )
| Expo ->
(fun v1 -> fun v2 -> int_of_float ((float_of_int v1) ** (float_of_int v2)))
;;
let rec eval_int (ctx : (string, int) contexte) (expr : (string, operateur) arbre_binaire) : int =
match expr with
| F(s) -> valeur ctx s
| N(t1, op, t2) ->
let v1, v2 = eval_int ctx t1, eval_int ctx t2 in
(intop_of_op op) v1 v2
;;
Par exemple, $x$ vaut $1$ dans le contexte d'exemple, et $x + y$ vaut $1 + 2 = 3$ :
let _ = eval_int contexte1 (F("x"));;
let _ = eval_int contexte1 (N(F("x"), Plus, F("y")));;
let _ = eval_int contexte1 exp1;;
let _ = eval_int contexte1 exp2;;
let _ = eval_int contexte1 exp3;;
On voit la faiblesse de l'interprétation avec des entiers, la division / est une division entière !
On peut aussi interpréter avec des flottants :
let contexte2 : (string, float) contexte = [
("x", 1.); ("y", 2.); ("z", 3.);
("u", 4.); ("v", 5.); ("w", 6.)
];;
let floatop_of_op (op : operateur) : (float -> float -> float) =
match op with
| Plus -> ( +. )
| Moins -> ( -. )
| MoinsDroite -> (fun v1 -> fun v2 -> v2 -. v1)
| Mul -> ( *. )
| Div -> ( /. )
| DivDroite -> (fun v1 -> fun v2 -> v2 /. v1)
| Modulo ->
(fun v1 -> fun v2 -> float_of_int ((int_of_float v1) mod (int_of_float v2)))
| Expo -> ( ** )
;;
let rec eval_float (ctx : (string, float) contexte) (expr : (string, operateur) arbre_binaire) : float =
match expr with
| F(s) -> valeur ctx s
| N(t1, op, t2) ->
let v1, v2 = eval_float ctx t1, eval_float ctx t2 in
(floatop_of_op op) v1 v2
;;
Par exemple, $x$ vaut $1$ dans le contexte d'exemple, et $x + y$ vaut $1 + 2 = 3$ :
let _ = eval_float contexte2 (F("x"));;
let _ = eval_float contexte2 (N(F("x"), Plus, F("y")));;
let _ = eval_float contexte2 exp1;;
let _ = eval_float contexte2 exp2;;
let _ = eval_float contexte2 exp3;;
Evaluation par lecture postfix et pile¶
On va commencer par lire l'arbre en parcours postfix (cf. TP2 @ ENS Rennes 2017/18) et ensuite l'évaluer grâce à une pile.
type ('a, 'b) lexem = O of 'b | V of 'a;;
type ('a, 'b) parcours = (('a, 'b) lexem) list;;
let parcours_postfix (expr : ('a, 'b) arbre_binaire) : (('a, 'b) parcours) =
let rec parcours vus expr =
match expr with
| F(s) -> V(s) :: vus
| N(t1, op, t2) -> O(op) :: (parcours (parcours vus t1) t2)
in
List.rev (parcours [] expr)
;;
On le teste :
parcours_postfix exp1;;
parcours_postfix exp3;;
let eval_int_2 (ctx : (string, int) contexte) (expr : (string, operateur) arbre_binaire) : int =
let vus = parcours_postfix expr in
let pile = Stack.create () in
let aux lex =
match lex with
| V(s) -> Stack.push (valeur ctx s) pile;
| O(op) ->
let v1, v2 = Stack.pop pile, Stack.pop pile in
Stack.push ((intop_of_op op) v1 v2) pile;
in
List.iter aux vus;
Stack.pop pile
;;
Par exemple, $x - y*z$ avec $x = 1, y = 2, z = 3$ vaut $1 - 2 * 3 = -5$ :
let _ = exp1 ;;
let _ = eval_int_2 contexte1 exp1;;
let _ = exp2;;
let _ = eval_int_2 contexte1 exp2;;
On peut maintenant faire la même fonction mais qui va en plus afficher l'état successif de la pile (avec des valeurs uniquement).
let print f =
let r = Printf.printf f in
flush_all();
r
;;
let print_pile pile =
print "\nPile : ";
Stack.iter (print "%i; ") pile;
print "."
;;
let eval_int_3 (ctx : (string, int) contexte) (expr : (string, operateur) arbre_binaire) : int =
let vus = parcours_postfix expr in
let pile = Stack.create () in
let aux lex =
print_pile pile;
match lex with
| V(s) -> Stack.push (valeur ctx s) pile;
| O(op) ->
let v1, v2 = Stack.pop pile, Stack.pop pile in
Stack.push ((intop_of_op op) v1 v2) pile;
in
List.iter aux vus;
Stack.pop pile
;;
let _ = exp1 ;;
let _ = eval_int_3 contexte1 exp1;;
let _ = exp3;;
let _ = eval_int_3 contexte1 exp3;;
Il y a un soucis dans l'ordre d'affichage des lignes, dû à Jupyter et pas à notre fonction.
On vérifie qu'on utilise au plus 4 valeurs sur la pile, comme représenté dans la figure de l'énoncé :
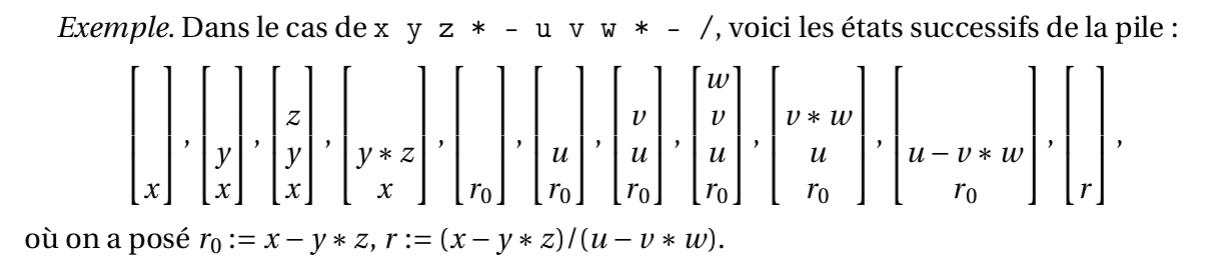
Affichage dans ce langage de manipulation de registre¶
On ne va pas trop formaliser ça, mais juste les afficher...
let print_aff (line : int) (i : int) (s : string) : unit =
print "\n%02i: R[%d] := %s ;" line i s;
;;
let string_of_op (op : operateur) : string =
match op with
| Plus -> "+"
| Moins | MoinsDroite -> "-"
| Mul -> "*"
| Div | DivDroite -> "/"
| Modulo -> "%"
| Expo -> "^"
;;
let print_op (line : int) (i : int) (j : int) (k : int) (op : operateur) : unit =
match op with
| MoinsDroite | DivDroite -> (* on gère ici les opérateurs "inverses" *)
print "\n%02i: R[%d] := R[%d] %s R[%d] ;" line i k (string_of_op op) j;
| _ ->
print "\n%02i: R[%d] := R[%d] %s R[%d] ;" line i j (string_of_op op) k;
;;
let eval_int_4 (ctx : (string, int) contexte) (expr : (string, operateur) arbre_binaire) : int =
let vus = parcours_postfix expr in
let pile = Stack.create () in
let ligne = ref 0 in
let aux lex =
incr ligne;
match lex with
| V(s) ->
Stack.push (valeur ctx s) pile;
print_aff !ligne ((Stack.length pile) - 1) s;
| O(op) ->
let v1, v2 = Stack.pop pile, Stack.pop pile in
Stack.push ((intop_of_op op) v1 v2) pile;
print_op !ligne ((Stack.length pile) - 1) ((Stack.length pile) - 1) (Stack.length pile) op;
in
List.iter aux vus;
Stack.pop pile
;;
Essayons ça :
let _ = exp1 ;;
let _ = eval_int_4 contexte1 exp1;;
let _ = exp3;;
let _ = eval_int_4 contexte1 exp3;;
Méthode d'Ershov¶
Enfin, on va générer, en plus de l'évaluation, un affichage comme celui qu'on voulait, qui montre les affectations dans les registres, et permettra de visualiser que la méthode d'Ershov utilise un registre de moins sur le terme exemple qui calcule $(x - y*z)/(u - v*w)$.
On rappelle qu'on a obtenu un arbre binaire décoré, représenté comme tel :
decore exp1;;
On modifie notre parcours postfix pour prendre en compte la décoration et savoir si on calcul d'abord le sous-arbre gauche ou droit.
let parcours_postfix_decore (expr : ('a, 'b, decoration) arbre_binaire_decore) : (('a, 'b) parcours) =
let rec parcours vus expr =
match expr with
| F2(s) -> V(s) :: vus
| N2(dec, t1, Moins, t2) when dec.premier_gauche = false ->
O(MoinsDroite) :: (parcours (parcours vus t2) t1)
| N2(dec, t1, MoinsDroite, t2) when dec.premier_gauche = false ->
O(Moins) :: (parcours (parcours vus t2) t1)
| N2(dec, t1, Div, t2) when dec.premier_gauche = false ->
O(DivDroite) :: (parcours (parcours vus t2) t1)
| N2(dec, t1, DivDroite, t2) when dec.premier_gauche = false ->
O(Div) :: (parcours (parcours vus t2) t1)
| N2(dec, t1, op, t2) when dec.premier_gauche = false ->
O(op) :: (parcours (parcours vus t2) t1)
| N2(_, t1, op, t2) ->
O(op) :: (parcours (parcours vus t1) t2)
in
List.rev (parcours [] expr)
;;
let eval_int_ershov (ctx : (string, int) contexte) (expr : (string, operateur) arbre_binaire) : int =
let vus = parcours_postfix_decore (decore expr) in
let pile = Stack.create () in
let ligne = ref 0 in
let aux lex =
incr ligne;
match lex with
| V(s) ->
Stack.push (valeur ctx s) pile;
print_aff !ligne ((Stack.length pile) - 1) s;
| O(op) ->
let v1, v2 = Stack.pop pile, Stack.pop pile in
Stack.push ((intop_of_op op) v1 v2) pile;
print_op !ligne ((Stack.length pile) - 1) ((Stack.length pile) - 1) (Stack.length pile) op;
in
List.iter aux vus;
Stack.pop pile
;;
Essayons ça :
let _ = exp1 ;;
let _ = eval_int_ershov contexte1 exp1;;
let _ = exp3;;
let _ = eval_int_ershov contexte1 exp3;;
Et voilà, ce n'était pas trop dur !
Conclusion¶
Voilà pour la question obligatoire de programmation, et un petit bonus.
Qualités¶
- On a décomposé le problème en sous-fonctions (d'abord le calcul de $\rho$ puis la méthode d'Ershov),
- On a fait des exemples et on les garde dans ce qu'on présente au jury,
- On a testé la fonction exigée sur de petits exemples et sur un exemple de taille réelle (venant du texte).
Bonus¶
On a fait pas mal de bonus, en interprétant les termes, d'abord via l'arbre et des appels récursifs, ensuite par une lecture postfix et une pile, qui nous a permis de vérifier l'évolution de la pile et de sa hauteur (avec le même exemple que dans le texte), et ensuite avec une espèce de "compilation" en visualisant les affectations dans ces registres. La "compilation" n'est pas réelle, on a uniquement affiché des choses, mais elle permet de vérifier que la méthode de Ershov aide effectivement à réduire le nombre de registre requis.
Défauts¶
- ?
Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive.
Vous auriez pu choisir de modéliser le problème avec une autre approche, n'hésitez pas à me contacter svp.
C'est tout pour aujourd'hui les amis, allez voir ici pour d'autres corrections, et que la force soit avec vous !