Index of /publis/slides/2017_12__Presentation_Inria_Lille_SequeL_Seminar
(StrapDown.js v0.8, theme united, thanks to BitBucket)

Index of /publis/slides/2017_12__Presentation_Inria_Lille_SequeL_Seminar

[ICO]NameLast modifiedSizeDescription
[PARENTDIR]Parent Directory  -  
[DIR]figures/2021-03-04 16:23 -  
[ ]slides.synctex.gz2021-03-04 16:23 114K 
[ ]slides.vrb2021-03-04 16:23 1.0K 
[TXT]README.md2021-03-04 16:23 16K 
[TXT]macrosText.sty2021-03-04 16:23 2.7K 
[TXT]preprocess_tex.sh2021-03-04 16:23 119  
[TXT]slides.html2021-03-04 16:23 18KMulti-Player Bandits Revisited | 22 Dec 2017 | Lilian Besson
[TXT]slides.md2021-03-04 16:23 29K 
[ ]slides.pdfpc2021-03-04 16:23 32  
[TXT]slides.tex2021-03-04 16:23 43K 
[ ]slides_169.pdfpc2021-03-04 16:23 36  
[TXT]slides_169.tex2021-03-04 16:23 44K 
[TXT]thomson_sampling_slides.md2021-03-04 16:23 933  
[ ]slides.pdf2021-03-04 16:23 1.1M 
[ ]slides.fls2021-03-04 16:23 41K 
[ ]slides_169.pdf2021-03-04 16:23 535K 
[ ]slides.aux2021-03-04 16:23 22K 
[ ]Makefile2021-03-04 16:23 1.3K 
[ ]slides.fdb_latexmk2021-03-04 16:23 38K 
[TXT]slides.log2021-03-04 16:23 112K 
[ ]slides.out2021-03-04 16:23 2.9K 
[ ]slides.nav2021-03-04 16:23 12K 
[ ]slides.toc2021-03-04 16:23 3.3K 
[ ]slides.snm2021-03-04 16:23 154  
[ ].gitignore2021-03-04 16:23 7  

author: Lilian Besson *Advised by Christophe Moy Émilie Kaufmann title: Multi-Player Bandits Models Revisited subtitle: Decentralized Multi-Player Multi-Arm Bandits institute: PhD Student, Team SCEE, IETR, CentraleSupélec, Rennes & Team SequeL, CRIStAL, Inria, Lille date: SequeL Seminar - 22 December 2017

lang: english

Motivation

We control some communicating devices, they want to access to a single base station.

Goal

How?

Outline and reference

  1. Introduction
  2. Our model: 3 different feedback levels
  3. Decomposition and lower bound on regret
  4. Quick reminder on single-player MAB algorithms
  5. Two new multi-player decentralized algorithms
  6. Upper bounds on regret for MCTopM
  7. Experimental results
  8. An heuristic (Selfish), and disappointing results
  9. Conclusion

This is based on our latest article:

Our model

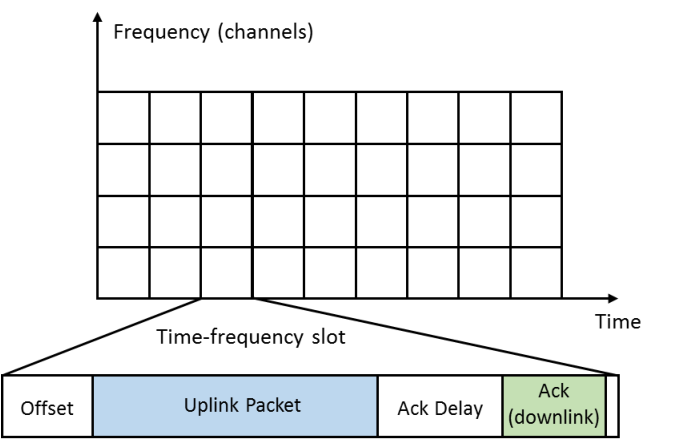
Protocol in time and frequency, with an Acknowledgement

Dynamic device = dynamic radio reconfiguration

Our model

"Easy" case

Two variants : with or without sensing

  1. With sensing: Device first senses for presence of Primary Users (background traffic), then use Ack to detect collisions. Model the "classical" Opportunistic Spectrum Access problem. Not exactly suited for Internet of Things, but can model ZigBee, and can be analyzed mathematically...

  2. Without sensing: same background traffic, but cannot sense, so only Ack is used. More suited for "IoT" networks like LoRa or SigFox. (Harder to analyze mathematically.)

Background traffic, and rewards

i.i.d. background traffic

Rewards

r^j(t) := Y_{A^j(t),t} × 1(not C^j(t)) = 1(uplink & Ack).

3 feedback levels

r^j(t)} := Y_{A^j(t),t} × 1(not C^j(t))

  1. "Full feedback": observe both Y_{A^j(t),t} and C^j(t) separately, → Not realistic enough, we don't focus on it.

  2. "Sensing": first observe Y{A^j(t),t}, then C^j(t) only if Y{A^j(t),t} != 0, → Models licensed protocols (ex. ZigBee), our main focus.

  3. "No sensing": observe only the joint Y_{A^j(t),t} × 1(not C^j(t)), → Unlicensed protocols (ex. LoRaWAN), harder to analyze !

But all consider the same instantaneous reward r^j(t).

Goal

Problem

Decentralized reinforcement learning optimization!

Centralized regret

A measure of success

Two directions of analysis

Lower bound

  1. Decomposition of regret in 3 terms,
  2. Asymptotic lower bound of one term,
  3. And for regret,
  4. Sketch of proof,
  5. Illustration.

Decomposition on regret

Decomposition

For any algorithm, decentralized or not, we have

RT(µ, M, rho) = sum{k in M-worst} (µM^* - µ_k) Eµ[Tk(T)] + sum{k in M-best} (µk - µ_M^*) (T - Eµ[Tk(T)]) + sum{k=1}^{K} µk Eµ[C_k(T)].

Small regret can be attained if...

  1. Devices can quickly identify the bad arms M-worst, and not play them too much (number of sub-optimal selections),
  2. Devices can quickly identify the best arms, and most surely play them (number of optimal non-selections),
  3. Devices can use orthogonal channels (number of collisions).

Asymptotic Lower Bound on regret

3 terms to lower bound...

Asymptotic Lower Bound on regret

Theorem 1 [Besson & Kaufmann, 2017]

Where kl(x,y) := x log(x / y) + (1 - x) log(1-x / 1-y) is the binary Kullback-Leibler divergence.

Remarks

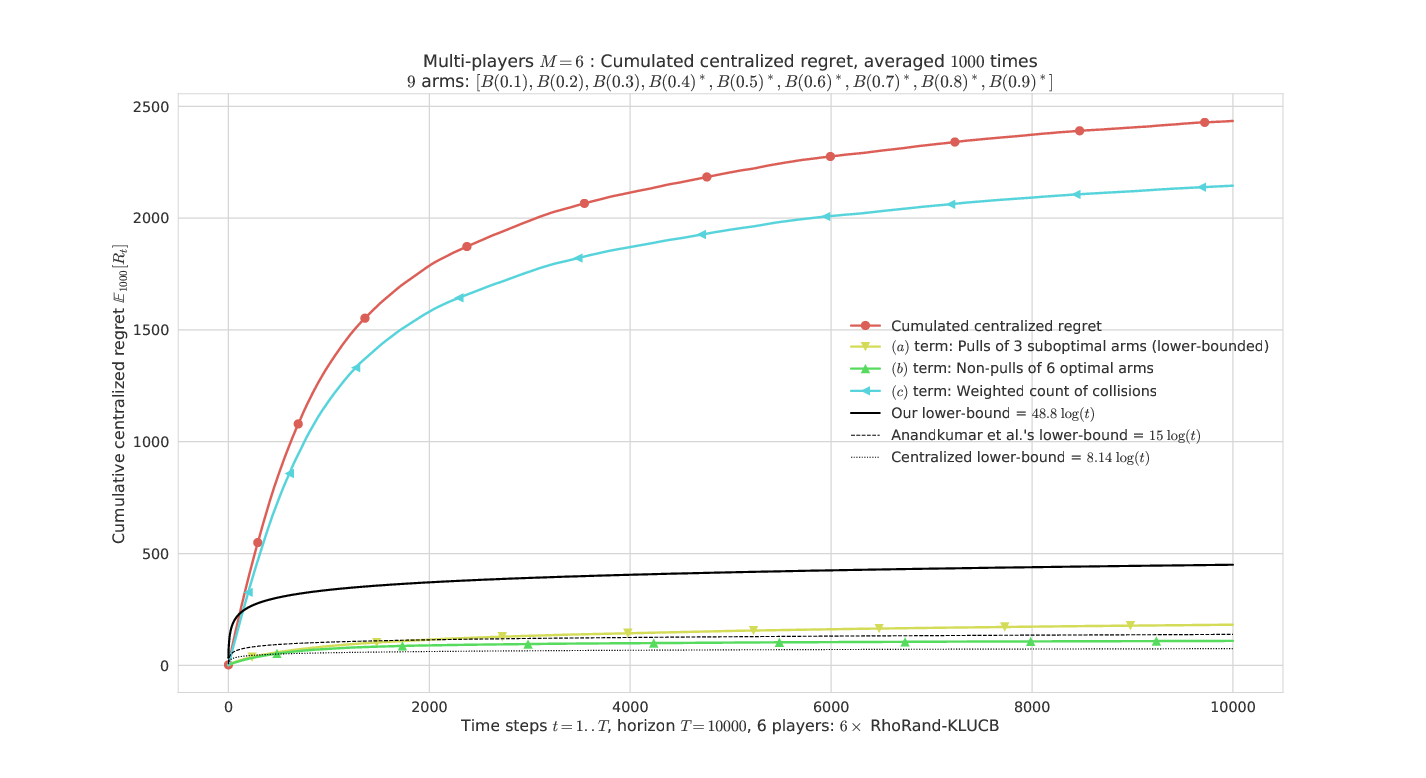
Illustration of the Lower Bound on regret

Any such lower bound is very asymptotic, usually not satisfied for small horizons. We can see the importance of the collisions!

Sketch of the proof

→ See our paper for details!

Single-player MAB algorithms

  1. Index-based MAB deterministic policies,
  2. Upper Confidence Bound algorithm : UCB,
  3. Kullback-Leibler UCB algorithm : klUCB.

Upper Confidence Bound algorithm UCB1

The device keep t number of sent packets, T_k(t) selections of channel k, X_k(t) successful transmissions in channel k.

  1. For the first K steps (t=1,...,K), try each channel once.
  2. Then for the next steps t > K :
    • Compute the index g_k(t) := X_k(t) / T_k(t) + sqrt{log(t) / 2 T_k(t)}
    • Choose channel A(t) = arg max_k g_k(t),
    • Update T_k(t+1) and X_k(t+1).

References: [Lai & Robbins, 1985], [Auer et al, 2002], [Bubeck & Cesa-Bianchi, 2012]

Kullback-Leibler UCB algorithm klUCB

The device keep t number of sent packets, T_k(t) selections of channel k, X_k(t) successful transmissions in channel k.

  1. For the first K steps (t=1,...,K), try each channel once.
  2. Then for the next steps t > K :
    • Compute the index gk(t) := sup{q in [a, b]} { q : kl(X_k(t) / T_k(t), q) <= log(t) / T_k(t) }
    • Choose channel A(t) = arg max_k g_k(t),
    • Update T_k(t+1) and X_k(t+1).

Why bother? klUCB is proved to be more efficient than UCB, and asymptotically optimal for single-player stochastic bandit.

References: [Garivier & Cappé, 2011], [Cappé & Garivier & Maillard & Munos & Stoltz, 2013]

Multi-player decentralized algorithms

  1. Common building blocks of previous algorithms,
  2. First proposal: RandTopM,
  3. Second proposal: MCTopM,
  4. Algorithm and illustration.

Algorithms for this easier model

Building blocks : separate the two aspects

  1. MAB policy to learn the best arms (use sensing Y_{A^j(t),t}),
  2. Orthogonalization scheme to avoid collisions (use C^j(t)).

Many different proposals for decentralized learning policies

Our proposals: [Besson & Kaufmann, 2017]

A first decentralized algorithm

The MCTopM algorithm

The RandTopM algorithm

The MCTopM algorithm

The MCTopM algorithm

The MCTopM algorithm

The MCTopM algorithm

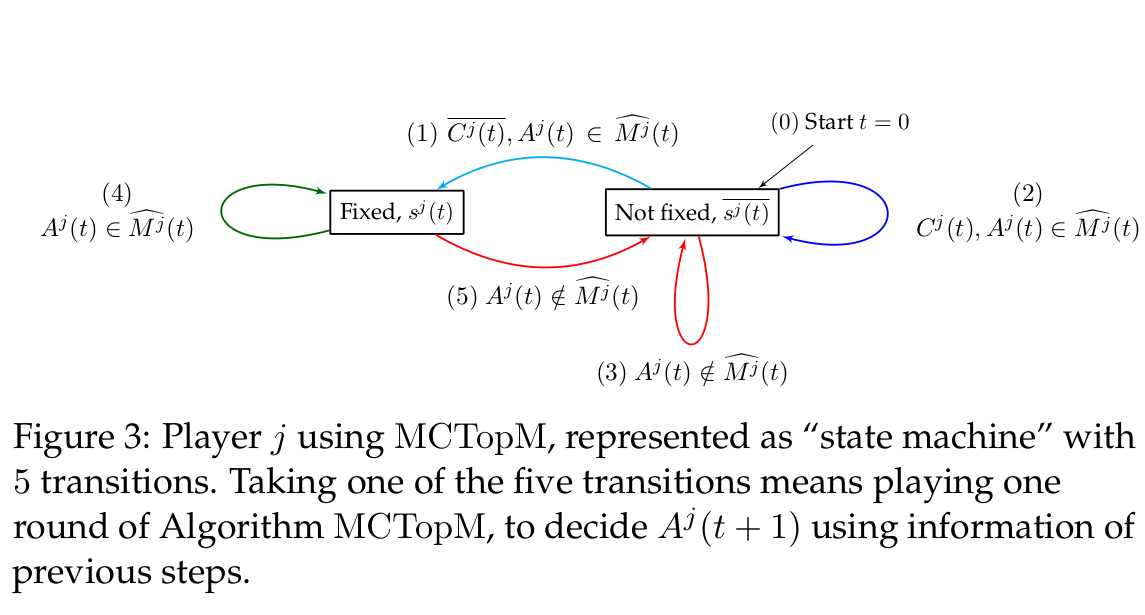
The MCTopM algorithm

Regret upper bound

  1. Theorem,
  2. Remarks,
  3. Idea of the proof.

Regret upper bound for MCTopM

Theorem 2 [Besson & Kaufmann, 2017]

How?

Regret upper bound for MCTopM

Remarks

Sketch of the proof

  1. Bound the expected number of collisions by M times the number of collisions for non-sitted players,
  2. Bound the expected number of transitions of type (3) and (5), by \bigO{\log T} using the klUCB indexes and the forced choice of the algorithm: gk^j(t-1) \leq g^j{k'}(t-1), and} gk^j(t) > g^j{k'}(t) when switching from k' to k,
  3. Bound the expected length of a sequence in the non-sitted state by a constant,
  4. So most of the times (O(T - log T)), players are sitted, and no collision happens when they are all sitted!

→ See our paper for details!

Experimental results

Experiments on Bernoulli problems µ in [0,1]^K.

  1. Illustration of regret for a single problem and M = K,
  2. Regret for uniformly sampled problems and M < K,
  3. Logarithmic number of collisions,
  4. Logarithmic number of arm switches,
  5. Fairness?

Constant regret if M = K

Regret, M=9 players, K=9 arms, horizon T=10000, 200 repetitions. Only RandTopM and MCTopM achieve constant regret in this saturated case (proved).

Illustration of regret of different algorithms

Regret, M=6 players, K=9 arms, horizon T=5000, against 500 problems µ uniformly sampled in [0,1]^K. Conclusion : rhoRand < RandTopM < Selfish < MCTopM in most cases.

Logarithmic number of collisions

Cumulated number of collisions. Also rhoRand < RandTopM < Selfish < MCTopM in most cases.

Logarithmic number of arm switches

Cumulated number of arm switches. Again rhoRand < RandTopM < Selfish < MCTopM, but no guarantee for rhoRand.

Fairness

Measure of fairness among player. All 4 algorithms seem fair in average, but none is fair on a single run It's quite hard to achieve both efficiency and single-run fairness!

An heuristic, Selfish

For the harder feedback model, without sensing.

  1. Just an heuristic,
  2. Problems with Selfish,
  3. Illustration of failure cases.

The Selfish heuristic

The Selfish decentralized approach = device don't use sensing, just learn on the reward (acknowledgement or not, r^j(t)).

Reference: [Bonnefoi & Besson et al, 2017]

Works fine...

But why would it work?

Works fine...

Illustration of failing cases for Selfish

Regret for M=2, K=3, T=5000, 1000 repetitions and µ = [0.1, 0.5, 0.9]. Axis x is for regret (different scale for each), and Selfish have a small probability of failure (17/1000 cases of R_T \gg \log T). The regret for the three other algorithms is very small for this "easy" problem.

Sum-up

Wait, what was the problem ?

Theoretical results

Other directions of future work

Conclude the Multi-Player OSA analysis

Extend to more objects M > K

Conclusion

We showed 😀

But more work is still needed... 😕

Thanks! 😀

Any question or idea ?