Multi-Player Bandits Revisited
Abstract
Multi-player Multi-Armed Bandits (MAB) have been extensively studied in the literature, motivated by applications to Cognitive Radio systems. Driven by such applications as well, we motivate the introduction of several levels of feedback for multi-player MAB algorithms. Most existing work assume that sensing information is available to the algorithm. Under this assumption, we improve the state-of-the-art lower bound for the regret of any decentralized algorithms and introduce two algorithms, and , that are shown to empirically outperform existing algorithms. Moreover, we provide strong theoretical guarantees for these algorithms, including a notion of asymptotic optimality in terms of the number of selections of bad arms. We then introduce a promising heuristic, called , that can operate without sensing information, which is crucial for emerging applications to Internet of Things networks. We investigate the empirical performance of this algorithm and provide some first theoretical elements for the understanding of its behavior.
Keywords:
Multi-Armed Bandits; Decentralized algorithms; Reinforcement learning; Cognitive Radio; Opportunistic Spectrum Access.
1Introduction
Several sequential decision making problems under the constraint of partial information have been studied since the 1950s under the name of Multi-Armed Bandit (MAB) problems [25]. In a stochastic MAB model, an agent is facing unknown probability distributions, called arms in reference to the arms of a one-armed bandit (or slot machine) in a casino. Each time she selects (or draws) an arm, she receives a reward drawn from the associated distribution. Her goal is to build a sequential selection strategy that maximizes the total reward received. A class of algorithms to solve this problem is based on Upper Confidence Bounds (UCB), first proposed by [21] and further popularized by [6]. The field has been very active since then, with several algorithms proposed and analyzed, both theoretically and empirically, even beyond the stochastic assumption on arms, as explained in the survey by [11].
The initial motivation to study MAB problems arose from clinical trials (the first MAB model can be traced back to , by [28]), in which a doctor sequentially allocates treatments (arms) to patients and observes their efficacy (reward). More recently, applications of MAB have shifted towards sequential content recommendation, e.g. sequential display of advertising to customers or A/B testing [22]. In the mean time, MAB were found to be relevant to the field of Cognitive Radio (CR, [24]), and [15] first proposed to use for the Opportunistic Spectrum Access (OSA) problem, and successfully conducted experiments on real radio networks demonstrating its usefulness. For CR applications, each arm models the quality or availability of a radio channel (a frequency band) in which there is some background traffic (e.g., primary users paying to have a guaranteed access to the channel in the case of OSA). A smart radio device needs to insert itself in the background traffic, by sequentially choosing a channel to access and try to communicate on, seeking to optimize the quality of its global transmissions.
For the development of CR, a crucial step is to insert multiple smart devices in the same background traffic. With the presence of a central controller that can assign the devices to separate channels, this amounts to choosing at each time step several arms of a MAB in order to maximize the global rewards, and can thus be viewed as an application of the multiple-play bandit, introduced by [5] and recently studied by [20]. Due to the communication cost implied by a central controller, a more relevant model is the decentralized multi-player multi-armed bandit model, introduced by [23] and [3], in which players select arms individually and collisions may occur, that yield a loss of reward. Further algorithms were proposed in similar models by [27] and [17] (under the assumption that each arm is a Markov chain) and by [8] and [26] (for i.i.d. or piece-wise i.i.d. arms). The goal for every player is to select most of the time one of the best arms, without colliding too often with other players. A first difficulty relies in the well-known trade-off between exploration and exploitation: players need to explore all arms to estimate their means while trying to focus on the best arms to gain as much rewards as possible. The decentralized setting considers no exchange of information between players, that only know and , and to avoid collisions, players should furthermore find orthogonal configurations (i.e., the players use the best arms without any collision), without communicating. Hence, in that case the trade-off is to be found between exploration, exploitation and low collisions.
All these above-mentioned works are motivated by the OSA problem, in which it is assumed that sensing occurs, that is each smart device observes the availability of a channel (sample from the arm) before trying to transmit and possibly experiment a collision with other smart devices. However some real radio networks do not use sensing at all, e.g., emerging standards developed for Internet of Things (IoT) networks such as LoRaWAN. Thus, to take into account these new applications, algorithms with additional contraints on the available feedback have to be proposed within the multiple-player MAB model. Especially, the typical approach that combines a (single-player) bandit algorithm based on the sensing information –to learn the quality of the channels while targeting the best ones– with a low-complexity decentralized collision avoidance protocol, is no longer possible.
In this paper, we take a step back and present the different feedback levels possible for multi-player MAB algorithms. For each of them, we propose algorithmic solutions supported by both experimental and theoretical guarantees. In the presence of sensing information, our contributions are a new problem-dependent regret lower bound, tighter than previous work, and the introduction of two algorithms, and . Both are shown to achieve an asymptotically optimal number of selections of the sub-optimal arms, and for we furthermore establish a logarithmic upper bound on the regret, that follows from a careful control of the number of collisions. In the absence of sensing information, we propose the heuristic and investigate its performance. Our study of this algorithm is supported by (promising) empirical performance and some first (disappointing) theoretical elements.
The rest of the article is organized as follows. We introduce the multi-player bandit model with three feedback levels in Section 2, and give a new regret lower bound in Section 3. The , and algorithms are introduced in Section 4, with the result of our experimental study reported in Section 5. Theoretical elements are then presented in Section 6.
2Multi-Player Bandit Model with Different Feedback Levels
We consider a -armed Bernoulli bandit model, in which arm is a Bernoulli distribution with mean . We denote the i.i.d. (binary) reward stream for arm , that satisfies and that is independent from the other rewards streams. However we mention that our lower bound and all our algorithms (and their analysis) can be easily extended to one-dimensional exponential families (just like for the algorithm of [12]). For simplicity, we focus on the Bernoulli case, that is also the most relevant for Cognitive Radio, as it can model channel availabilities.
In the multi-player MAB setting, there are players (or agents), that have to make decisions at some pre-specified time instants. At time step , player selects an arm , independently from the other players’ selections. A collision occurs at time if at least two players choose the same arm. We introduce the two events, for and
that respectively indicate that a collision occurs at time for player and that a collision occurs at time on arm . Each player then receives (and observes) the binary rewards ,
In words, she receives the reward of the selected arm if she is the only one to select this arm, and a reward zero otherwise
A multi-player MAB strategy is a tuple of arm selection strategies for each player, and the goal is to propose a strategy that maximizes the total reward of the system, under some constraints. First, each player should adopt a sequential strategy , that decides which arm to select at time based on previous observations. Previous observations for player at time always include the previously chosen arms and received rewards for , but may also include the sensing information or the collision information . More precisely, depending on the application, one may consider the following three observation models, (I), (II) and (III).
(I) Simultaneous sensing and collision
Player observes and (not previously studied).
(II) Sensing, then collision
Player observes , then observes the reward, and thus also only if . This common setup, studied for example by [4], is relevant to model the OSA problem: the device first checks for the presence of primary users in the chosen channel. If this channel is free (), the transmission is successful () if no collision occurs with other smart devices ().
(III) No sensing
Player only observes the reward . For IoT networks, this reward can be interpreted as an acknowledgement from a Base Station, received when a communication was successful. A lack of acknowledgment may be due to a collision with a device from the background traffic , or to a collision with one of the others players (). However, the sensing and collision information are censored. Recently, [10] presented the first (bandit-based) algorithmic solutions under this (harder) feedback model, in a slightly different setup, more suited to large scale IoT applications.
Under each of these three models, we define to be the filtration generated by the observations gathered by player up to time (which contains different information under models (I), (II) and (III)). While a centralized algorithm may select the vector of actions for all players based on all the observations from , under a decentralized algorithm the arm selected at time by player only depends on the past observation of this player. More formally, is assumed to be -measurable.
Definition 1 We denote by the best mean, the second best etc, and by the (non-sorted) set of the indices of the arms with largest mean (best arms): if then . Similarly, denotes the set of indices of the arms with smallest means (worst arms), . Note that they are both uniquely defined if .
Following a natural approach in the bandit literature, we evaluate the performance of a multi-player strategy using the expected regret, that measures the performance gap with respect to the best possible strategy. The regret of the strategy at horizon is the difference between the cumulated reward of an oracle strategy, assigning in this case the players to , and the cumulated reward of strategy :
Maximizing the expected sum of global reward of the system is indeed equivalent to minimizing the regret, and we now investigate the best possible regret rate of a decentralized multi-player algorithm.
3An Asymptotic Regret Lower Bound
In this section, we provide a useful decomposition of the regret (Lemma 1) that permits to establish a new problem-dependent lower bound on the regret (Theorem 1), and also provides key insights on the derivation of regret upper bounds (Lemma 3).
3.1A Useful Regret Decomposition
We introduce additional notations in the following definition.
Definition 2 Let , and denote the number of selections of arm by any player , up to time .
Let be the number of colliding players
Letting be the set of bandit instances such that there is a strict gap between the best arms and the other arms, we now provide a regret decomposition for any .
Lemma 1 For any bandit instance such that , it holds that (Proved in Appendix A.1)
In this decomposition, term (a) counts the lost rewards due to sub-optimal arms selections (), term (b) counts the number of times the best arms were not selected (), and term (c) counts the weighted number of collisions, on all arms. It is valid for both centralized and decentralized algorithms. For centralized algorithms, due to the absence of collisions, (c) is obviously zero, and (b) is non-negative, as . For decentralized algorithms, (c) may be significantly large, and term (b) may be negative, as many collisions on arm may lead to . However, a careful manipulation of this decomposition (see Appendix A.2) shows that the regret is always lower bounded by term (a).
Lemma 2 For any strategy and , it holds that .
3.2An Improved Asymptotic Lower Bound on the Regret
To express our lower bound, we need to introduce as the Kullback-Leibler divergence between the Bernoulli distribution of mean and that of mean , so that We first introduce the assumption under which we derive a regret lower bound, that generalizes a classical assumption made by [21] in single-player bandit models.
Definition 3 A strategy is strongly uniformly efficient if for all and for all ,
Having a small regret on every problem instance, i.e., uniform efficiency, is a natural assumption for algorithms, that rules out algorithms tuned to perform well on specific instances only. From this assumption and the decomposition of Lemma 1 one can see
The additional assumption in further implies some notion of fairness, as it suggests that each of the players spends on average the same amount of time on each of the best arms. Note that this assumption is satisfied by any strategy that is invariant under every permutation of the players, i.e., for which the distribution of the observations under is independent from the choice of permutation . In that case, it holds that for every arm and , hence and are equivalent, and strong uniform efficiency is equivalent to standard uniform efficiency. Note that all our proposed algorithms are permutation invariant and is thus an example of strongly uniformly efficient algorithm, as we prove in Section 6 that its regret is logarithmic on every instance .
We now state a problem-dependent asymptotic lower bound on the number of sub-optimal arms selections under a decentralized strategy that has access to the sensing information. This result, proved in Appendix B, yields an asymptotic logarithmic lower bound on the regret, also given in Theorem 1.
Theorem 1 Under observation models and , for any strongly uniformly efficient decentralized policy and ,
From Lemma 2, it follows that
Observe that the regret lower bound is tighter than the state-of-the-art lower bound in this setup given by [23], that states that
as for every and , (see Figure 7 in Appendix F.1). It is worth mentioning that [23] proved a lower bound under the more general assumption for that there exists some numbers such that whereas in Definition ? we make the choice . Our result could be extended to this case but we chose to keep the notation simple and focus on fair allocation of the optimal arms between players.
Interestingly, our lower bound is exactly a multiplicative constant factor away from the lower bound given by [5] for centralized algorithms (which is clearly a simpler setting). This intuitively suggests the number of players as the (multiplicative) “price of decentralized learning”. However, to establish our regret bound, we lower bounded the number of collisions by zero, which may be too optimistic. Indeed, for an algorithm to attain the lower bound , the number of selections of each sub-optimal arm should match the lower bound and term (b) and term (c) in the regret decomposition of Lemma 1 should be negligible compared to . To the best of our knowledge, no algorithm has been shown to experience only collisions so far, for every and .
A lower bound on the minimal number of collisions experienced by any strongly uniformly efficient decentralized algorithm would thus be a nice complement to our Theorem 1, and it is left as future work.
3.3Towards Regret Upper Bounds
A natural approach to obtain an upper bound on the regret of an algorithm is to upper bound separately each of the three terms defined in Lemma 1. The following result shows that term can be related to the number of sub-optimal selections and the number of collisions that occurs on the best arms.
Lemma 3 The term in Lemma 1 is upper bounded as (Proved in Appendix A.3)
This result can also be used to recover Proposition 1 from [4], giving an upper bound on the regret that only depends on the expected number of sub-optimal selections – for – and the expected number of colliding players on the optimal arms – for . Note that, in term (c) the number of colliding players on the sub-optimal arm may be upper bounded as .
In the next Section, we present an algorithm that has a logarithmic regret, while ensuring that the number of sub-optimal selections is matching the lower bound of Theorem 1.
4New Algorithms for Multi-Player Bandits
When sensing is possible, that is under observation models (I) and (II), most existing strategies build on a single-player bandit algorithm (usually an index policy) that relies on the sensing information, together with an orthogonalization strategy to deal with collisions. We present this approach in more details in Section 4.1 and introduce two new algorithms of this kind, and . Then, we suggest in Section 4.2 a completely different approach, called , that no longer requires an orthogonalization strategy as the collisions are directly accounted for in the indices that are used. can also be used under observation model (III) –without sensing–, and without the knowledge of .
4.1Two New Strategies Based on Indices and Orthogonalization: and
In a single-player setting, index policies are popular bandit algorithms: at each round one index is computed for each arm, that only depends on the history of plays of this arm and (possibly) some exogeneous randomness. Then, the arm with highest index is selected. This class of algorithms includes the UCB family, in which the index of each arm is an Upper Confidence Bound for its mean, but also some Bayesian algorithms like Bayes-UCB [18] or the randomized Thompson Sampling algorithm [28].
The approaches we now describe for multi-player bandits can be used in combination with any index policy, but we restrict our presentation to UCB algorithms, for which strong theoretical guarantees can be obtained. In particular, we focus on two types of indices: indices [6] and indices [12], that can be defined for each player in the following way. Letting the current sum of sensing information obtained by player for arm , (if ) is the empirical mean of arm for player and one can define the index
where is some exploration function. is usually taken to be in practice, and slightly larger in theory, which ensures that (see [12]). A classical (single-player) UCB algorithm aims at the arm with largest index. However, if each of the players selects the arm with largest UCB, all the players will end up colliding most of the time on the best arm. To circumvent this problem, several coordination mechanisms have emerged, that rely on ordering the indices and targeting one of the -best indices.
While the algorithm [23] relies on the player agreeing in advance on the time steps at which they will target each of the best indices (even though some alternative without pre-agreement are proposed), the algorithm [4] relies on randomly selected ranks. More formally, letting be the index of the -th largest entry in a vector , in each player maintains at time an internal rank and selects at time ,
If a collision occurs, a new rank is drawn uniformly at random: .
We now propose two alternatives to this strategy, that do not rely on ranks and rather randomly fix themselves on one arm in , that is defined as the set of arms that have the largest indices:
Our proposal is stated below as Algorithm Figure 1, while a simpler variant, called , is stated as Algorithm Figure 4 in Appendix C. We focus on as it is easier to analyze and performs better. Both algorithms ensure that player always selects at time an arm from . When a collision occurs randomly switches arm within , while uses a more sophisticated mechanism, that is reminiscent of “Musical Chair” (MC) and inspired by the work of [26]: players tend to fix themselves on arms (“chairs”) and ignore future collision when this happens.

More precisely, under , if player did not encounter a collision when using arm at time , then she marks her current arm as a “chair” (), and will keep using it even if collisions happen in the future (Lines -). As soon as this “chair” is no longer in , a new arm is sampled uniformly from a subset of , defined with the previous indices (Lines -). The subset enforces a certain inequality on indices, and , when switching from to . This helps to control the number of such changes of arm, as shown in Lemma 5. The considered subset is never empty as it contains at least the arm replacing the in . Collisions are dealt with only for non-fixed player , and when the previous arm is still in . In this case, a new arm is sampled uniformly from (Lines -). This stationary aspect helps to minimize the number of collisions, as well as the number of switches of arm. The five differents transitions ,,,, refer to the notations used in the analysis of (see Figure 5 in Appendix D.3).
4.2The Approach
Under observation model (III) no sensing information is available and the previous algorithms cannot be used, as the sum of sensing information and thus the empirical mean cannot be computed, hence neither the indices . However, one can still define a notion of empirical reward received from arm by player , by introducing
Note that is no longer meant to be an unbiased estimate of as it also takes into account the collision information, that is present in the reward. Based on this empirical reward, one can similarly defined modified indices as
Given any of these two index policies ( or ), the algorithm is defined by,
The name comes from the fact that each player is targeting, in a “selfish” way, the arm that has the highest index, instead of accepting to target only one of the best. The reason that this may work precisely comes from the fact that is no longer an upper-confidence on , but some hybrid index that simultaneously increases when a transmission occurs and decreases when a collision occurs.
This behavior is easier to be understood for the case of - in which, letting be the number of collisions on arm , one can show that the hybrid index induces a penalty proportional to the fraction of collision on this arm and the quality of the arm itself:
From a bandit perspective, it looks like each player is using a stochastic bandit algorithm ( or ) when interacting with arms that give a feedback (the reward, and not the sensing information) that is far from being i.i.d. from some distribution, due to the collisions. As such, the algorithm does not appear to be well justified, and one may rather want to use adversarial bandit algorithms like [7], that do not require a stochastic (i.i.d.) assumption on arms. However, we found out empirically that is doing surprisingly well, as already noted by [10], who did some experiments in the context of IoT applications. We show in Section 6 that does have a (very) small probability to fail (badly), for some problem with small , which precludes the possibility of a logarithmic regret for any problem. However, in most cases it empirically performs similarly to all the algorithms described before, and usually outperforms , even if it neither exploits the sensing information, nor the knowledge of the number of players . As such, practitioners may still be interested by the algorithm, especially for Cognitive Radio applications in which sensing is hard or not considered.
5Empirical performances
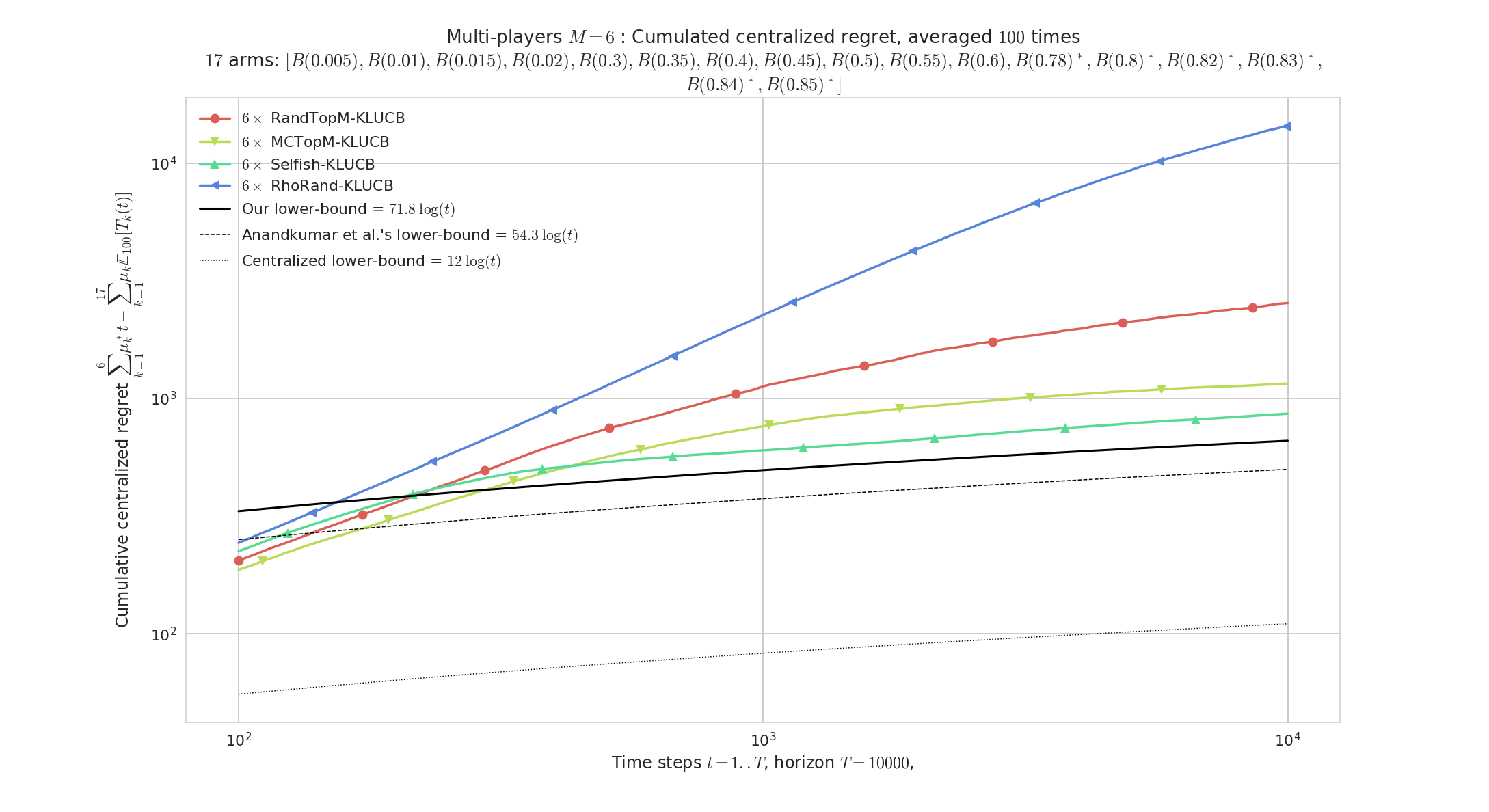
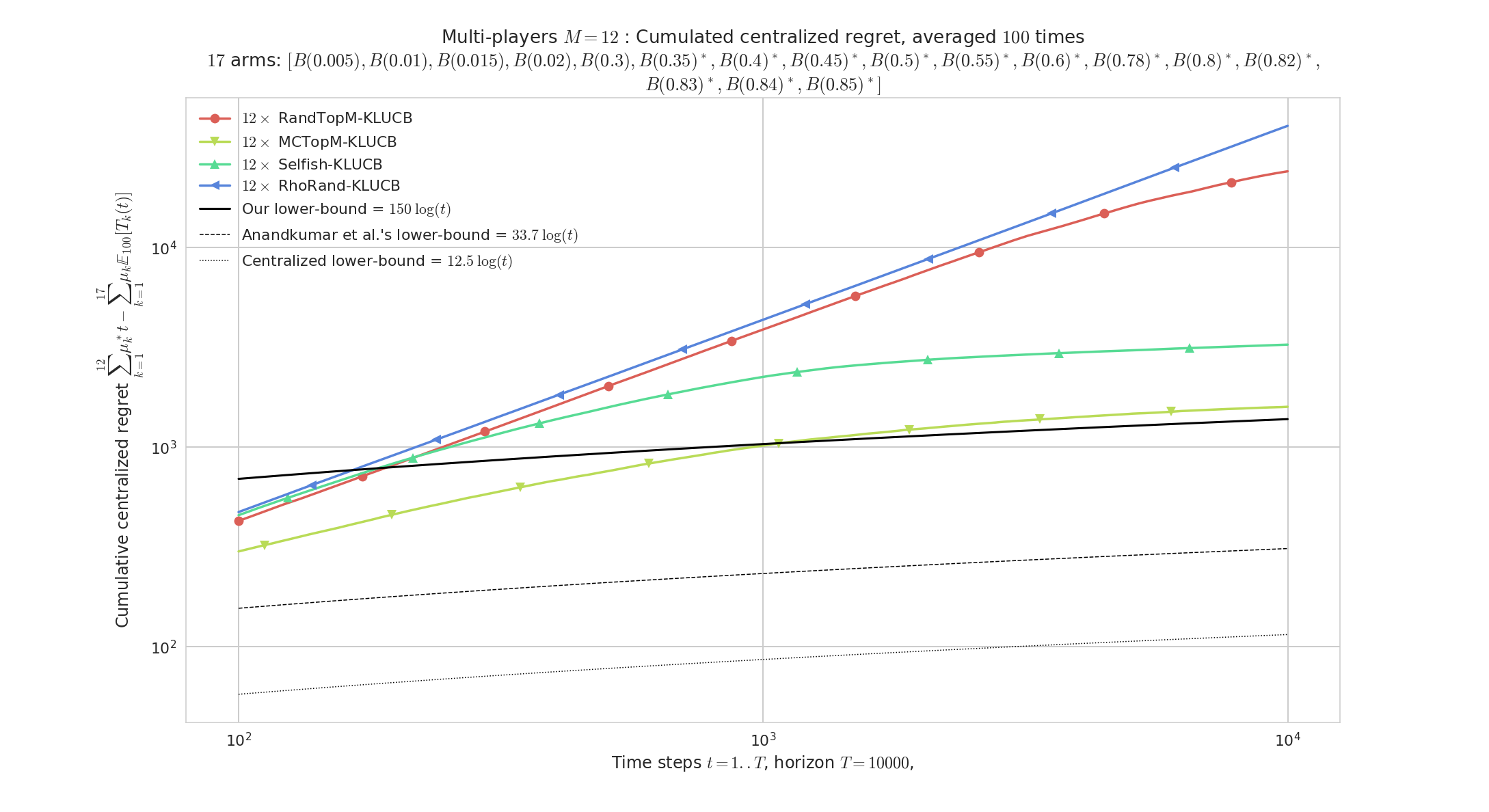
We illustrate here the empirical performances of the algorithms presented in Section 4, used with two index policies, and . Some plots are at pages and and most of them in Appendix F.2.
As expected, the same algorithm always performs better using rather than , as the theoretical guarantees for single player suggested, and the main goal of this work is not to optimize on the index policy but rather propose new ways of using indices, in a decentralized setting
Performance is measured using the average regret, with repetitions on the same problem, from to the horizon (also unknown by the algorithms), but we also include histograms showing the distribution of regret at , as this allows to check if the regret is indeed small for each run of the simulation. For the plots showing the regret, our asymptotic lower bound from Theorem 1 is displayed.
Experiments with a different problem for each repetition (uniformly sampled ), are also considered, in Figure 2 and Figure 12. This helps to check that no matter the complexity of the considered problem (one measure of complexity being the constant in our lower bound), performs similarly or better than all the other algorithms, and outperforms in most cases. Figure 2 is a good example of outstanding performances of and in comparison to .
![fig: Figure 2: Regret, M=6 players, K=9 arms, horizon T=5000, against 500 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. \mathrm{Rho}\mathrm{Rand} (top blue curve) is outperformed by the other algorithms (and the gain increases with M). \mathrm{MCTopM} (bottom yellow) outperforms all the other algorithms is most cases.](figures/MP__K9_M6_T5000_N500__4_algos/all_RegretCentralized____env1-1_8318947830261751207.png)
Empirically, our proposals were found to almost always outperform , and except for that can fail badly on problems with small , we verified that outperforms the state-of-the-art algorithms in many different problems, and is more and more efficient as and grows.
Two other multi-player multi-armed bandits algorithms are by [8] and by [26], that were proposed for the observation model (II). We chose to not include comparisons with any of them, as they were both found hard to use efficiently in practice. Indeed, needs a careful tuning of five parameters (, , , and ) to attain reasonable performances (and using cross validation, as the authors suggested, is usually considered out of the scope of online sequential learning). was shown to attain a constant regret (with high probability) only for very large horizons, and empirically it requires a fine tuning of its parameter , as the theoretical value requires to know the small gap between two arms, unavailable in practice.
![fig: Figure 3: Regret (in \log\log scale), for M=6 players for K=9 arms, horizon T=5000, for 1000 repetitions on problem \boldsymbol{\mu}=[0.1,\dots,0.9]. \mathrm{RandTopM} (yellow curve) outperforms \mathrm{Selfish} (green), both clearly outperform \mathrm{Rho}\mathrm{Rand}. The regret of \mathrm{MCTopM} is logarithmic, empirically with the same slope as the lower bound. The x axis on the regret histograms have different scale for each algorithm.](figures/MP__K9_M6_T10000_N1000__4_algos/all_RegretCentralized_loglog____env1-1_8200873569864822246.png)
![fig: Regret (in \log\log scale), for M=6 players for K=9 arms, horizon T=5000, for 1000 repetitions on problem \boldsymbol{\mu}=[0.1,\dots,0.9]. \mathrm{RandTopM} (yellow curve) outperforms \mathrm{Selfish} (green), both clearly outperform \mathrm{Rho}\mathrm{Rand}. The regret of \mathrm{MCTopM} is logarithmic, empirically with the same slope as the lower bound. The x axis on the regret histograms have different scale for each algorithm.](figures/MP__K9_M6_T10000_N1000__4_algos/all_HistogramsRegret____env1-1_8200873569864822246.png)
6Theoretical elements
Section 6.1 gives an asymptotically optimal analysis of the expected number of sub-optimal draws for , and combined with indices, and Section 6.2 proves that the number of collisions, hence the regret of are also logarithmic. Section 6.3 shortly discusses a disappoiting result regarding , with more insights provided in Appendix E.
6.1Common Analysis for - and -
Lemma 4 gives a finite-time upper bound on the expected number of draws of a sub-optimal arm for any player , that holds for both - and -. Our improved analysis also applies to the algorithm. Explicit formulas for , are in the proof in Appendix D.1.
Lemma 4 For any , if player uses the -, - or - decentralized policy with exploration function , then for any sub-optimal arm , there exists two problem depend constants , such that
It is important to notice that the leading constant in front of is the same as in the constant featured in Equation of Theorem 1. This result proves that the lower bound on sub-optimal selections is asymptotically matched for the three considered algorithms. This is a strong improvement in comparison to the previous state-of-the-art results [23].
As announced, Lemma 5 controls the number of switches of arm that are due to the current arm leaving , for both and . It essentially proves that Lines - in Algorithm Figure 1 (when a new arm is sampled from the non-empty subset of ) happen a logarithmic number of times. The proof of this result is given in Appendix D.2.
Lemma 5 For any , any player using - or -, and any arm , it holds that
6.2Regret Analysis of -
For , we are furthermore able to obtain a logarithmic regret upper bound, by proposing an original approach to control the number of collisions under this algorithm. First, we can bound the number of collisions by the number of collisions for players not yet “fixed on their arms” (), that we can then bound by the number of changes of arms (cf proof in Appendix D.3). An interesting consequence of the proof of this result is that it also bounds the number of switches of arms, , and this additional guarantee was never clearly stated for previous state-of-the-art works, like . Even though minimizing switching was not a goal
Lemma 6 For any , if all players use the - decentralized policy, and , then the total average number of collisions (on all arms) is upper-bounded by (Proved in Appendix D.3)
Note that this bound is in , which is significantly better than proved by [4] for . But it is worse than for proved by [26], due to our trick of focusing on collisions for non-sitted players.
Now that the sub-optimal arms selections and the collisions are both proved to be at most logarithmic in Lemmas 4 and 5, it follows from our regret decomposition (Lemma 1) together with Lemma 3 that the regret of - is logarithmic. More precisely, one obtains a finite-time problem-depend upper bound on the regret of this algorithm.
Theorem 2 If all players use -, and , then for any problem , there exists a problem dependent constant , such that the regret satisfies:
6.3Discussion on
The analysis of is harder, but we tried our best to obtain some understanding of the behavior of this algorithm, that seems to be doing surpisingly well in many contexts, as in our experiments with arms and in extensive experiments not reported in this paper. However, a disappointing result is that we found simple problems, usually with small number of arms, for which the algorithm may fail. For example with or players competing for arms, with means , the histograms in Figure 9 suggests that with a small probability, the regret of - can be very large. We provide a discussion in Appendix E about when such situations may happen, including a conjectured (constant, but small) lower bound on the probability that experience collision almost at every round. This result would then prevent from having a logarithmic regret. However, it is to be noted that the lower bound of Theorem 1 does not apply to the censored observation model (III) under which operates, and it is not known yet whether logarithmic regret is at all possible.
7Conclusion and future work
To summarize, we presented three variants of Multi-Player Multi-Arm Bandits, with different level of feedback being available to the decentralized players, under which we proposed efficient algorithms. For the two easiest models –with sensing–, our theoretical contribution improves both the state-of-the-art upper and lower bounds on the regret. In the absence of sensing, we also provide some motivation for the practical use of the interesting heuristic, a simple index policy based on hybrid indices that are directly taking into account the collision information.
This work suggests several interesting further research directions. First, we want to investigate the notion of optimal algorithms in the decentralized multi-player model with sensing information. So far we provided the first matching upper and lower bound on the expected number of sub-optimal arms selections, which suggests some form of (asymptotic) optimality. However, sub-optimal draws turn out not be the dominant terms in the regret, both in our upper bounds and in practice, thus an interesting future work is to identify some notion of minimal number of collisions. Second, it remains an open question to know if a simple decentralized algorithm can be as efficient as without knowing in advance, or in dynamic settings (when can change in time). We shall start by proposing variants of our algorithm that are inspired by the variant of proposed by [4]. Finally, we want to strengthen the guarantees obtained in the absence of sensing, that is to know whether logarithmic regret is achievable and to have a better analysis of the approach. Indeed, in most cases, it performs comparably to even with limited feedback and without knowing the number of players , which makes it a good candidate for applications to Internet of Things networks.
ARegret Decomposisions
a.1Proof of Lemma 1
Using the definition of regret from , and this collision indicator ,
The last equality comes from the linearity of expectations, and the fact that (for all , from the i.i.d. hypothesis), and the independence from , and (observed after playing ). So . And so
For the first term, we have , and if we denote the average mean of the -best arms, then,
Let be the gap between the mean of the arm and the -best average mean, and if denotes the index of the worst of the -best arms (i.e., ), then by splitting into three disjoint sets , we get
But for , , so by recombining the terms, we obtain,
The term simplifies to , and so by definition of . And for , , so the first sum can be written for only, so
And so we obtain the decomposition with three terms (a), (b) and (c).
a.2Proof of Lemma 2
Note that term (c) is clearly lower bounded by but it is not obvious for (b) as there is no reason for to be upper bounded by . Let , where the notation stands for “there exists a unique”. Then can be decomposed as
By focusing on the two terms from the decomposition of from Lemma 1, we have
And now both terms are non-negative, as , , and , so which proves that , as wanted.
a.3Proof of Lemma 3
Recall that we want to upper bound . First, we observe that, for all ,
where we denote by the set of selected arms at time (with no repetition). With this notation one can write
The quantity counts the number of optimal arms that have not been selected at time . For each mis-selection of an optimal arm, there either exists a sub-optimal arm that has been selected, or an arm in on which a collision occurs. Hence
which yields
and Lemma 3 follows.
BLower Bound: Proof of Theorem 1
b.1Proof of Theorem 1
The lower bound that we present relies on the following change-of-distribution lemma that we prove in the next section, following recent arguments from [14] that have to be adapted to incorporate the collision information.
Lemma 6 Under observation model (I) and (II), for every event that is -measurable, considering two multi-player bandit models denoted by and respectively, it holds that
Let be a sub-optimal arm under , fix , and let be the bandit instance such that
Clearly, also, and the set of best arms under and differ by one arm: if then . Thus, one expects the (-mesurable) event
to have a small probability under (under which is sub-optimal) and a large probability under (under which is one of the optimal arms, and is likely to be drawn a lot).
Applying the inequality in Lemma ?, and noting that the sum in the left-hand side reduces to on term as there is a single arm whose distribution is changed, one obtains
using the fact that the binary KL-divergence satisfies as well as the inequality , proved by [14]. Now, using Markov inequality yields
which defines two sequences and , such that
The strong uniform efficiency assumption (see Definition ?) further tells us that (as for all ) and when , for all . As a consequence, observe that when tends to infinity and
tends to one when tends to infinity. From Equation , this yields
for all . Letting go to zero gives the conclusion (as is continuous).
b.2Proof of Lemma
Under observation model (I) and (II), the strategy decides which arm to play based on the information contained in , where and
where denotes the sensing information, denotes the collision information (not always completely exploited under observation model (II)) and denotes some external source of randomness
Under two bandit models and , we let (resp. ) be the distribution of the observations under model (resp. ), given a fixed algorithm. Using the exact same technique as [14] (the contraction of entropy principle), one can establish that for any event that is -measurable
The next step is to relate the complicated KL-divergence to the number of arm selections. Proceeding similarly as [14], one can write, using the chain rule for KL-divergence, that
Now observe that conditionally to , , and are independent, as once the selected arm is known, the value of the sensing does not influence the other players selecting that arm, and is some exogenous randomness. Using further that the distribution of is the same under and , one obtains
The first term in can be rewritten using the same argument as [14], that relies on the fact that conditionally to , is a Bernoulli distribution with mean under the instance and under the instance :
We now show that second term in is zero:
where denote the information available to player . Knowing the information available to all other players player is an almost surely constant random variable, whose distribution is the same under and . Hence the inner expectation is zero and so does .
Putting things together, we showed that
Iterating this equality and using that yields that
for all , in particular for all .
CThe algorithm
We now state precisely the algorithm below in Algorithm Figure 4 (page ). It is essentially the same algorithm as , but in a simpler version as the “Chair” aspect is removed, that is, there is no notion of state (cf Algorithm Figure 1). Player is always considered “not fixed”, and a collision always forces a uniform sampling of the next arm from in the case of .

DProofs Elements Related to Regret Upper Bounds
This Appendix includes the main proofs, missing from the content of the article, that yield the regret upper bound. We start by controlling the sub-optimal draws when the indices are used (instead of ), with any of our proposed algorithms (, ) or . Then we focus on controlling collisions for -.
d.1Control of the Sub-optimal Draws for : Proof of Lemma 4
Fix and a player . The key observation is that for , as well as the algorithm, it holds that
Indeed, for the three algorithms, an arm selected at time belongs to the set of arms with largest indices. If the sub-optimal arm is selected at time , it implies that , and, because there are arms in both and , one of the arms in must be excluded from . In particular, the index of arm must be larger than the index of this particular arm .
Using , one can then upper bound the number of selections of arm by user up to round as
Considering the relative position of the upper-confidence bound and the corresponding mean , one can write the decomposition
where the last inequality (for the first term) comes from the fact that is the smallest of the for .
Now each of the two terms in the right hand side can directly be upper bounded using tools developed by [12] for the analysis of kl-UCB. The rightmost term can be controlled using Lemma 7 below that relies on a self-normalized deviation inequality, whose proof exactly follows from the proof of Fact 1 in Appendix A of [12]. The leftmost term can be controlled using Lemma 8 stated below, that is a direct consequence of the proof of Fact 2 in Appendix A of [12].
Lemma 7 For any arm , if is the index with exploration function ,
Denote the derivative of the function (for any fixed ).
Lemma 8 For any arms and such that , if is the kl-UCB index with exploration function ,
Putting things together, one obtains the non-asymptotic upper bound
which yields Lemma 4, with explicit constants and .
d.2Proof of Lemma 5
Using the behavior of the algorithm when the current arm leaves the set (Line 4), one has
Now, to control , we distinguish two cases. If , one can write
The first term in the right hand side is by Lemma 7. To control the second term, we apply the same trick that led to the proof of Lemma 8 in [12]. Letting , and be the empirical mean of the first observations from arm by player , one has
where the last inequality uses that for all ,
From , the same upper bound as that of Lemma 8 can be obtained using the tools from [12], which proves that for ,
If , we rather use that
and similarly Lemma 7 and a slight variant of Lemma 8 to deal with the modified time indices yields
Summing over yields the result.
d.3Controlling Collisions for : Proof of Lemma 5
A key feature of both the and algorithms is Lemma 5, that states that the probability of switching from some arm because this arm leaves is small. Its proof is postponed to the end of this section.
Figure 5 below provides a schematic representation of the execution of the algorithm, that has to be exploited in order to properly control the number of collisions. The sketch of the proof is the following: by focusing only on collisions in the “not fixed” state, bounding the number of transitions and is enough. Then, we show that both the number of transitions and are small: as a consequence of Lemma 5, the average number of these transitions is . Finally, we use that the length of a sequence of consecutive transitions is also small (on average smaller than ), and except for possibly the first one, starting a new sequence implies a previous transition or to arrive in the state “not fixed”. This gives a logarithmic number of transitions and , and so gives , with explicit constants depending on and .

As in Algorithm Figure 1, is the event that player decided to fix herself on an arm at the end of round . Formally, is false, and is defined inductively from as
For the sake of clarity, we now explain Figure 5 in words. At step , if player is not fixed (), she can have three behaviors when executing . She keeps the same arm and goes to the other state with transition , or she stays in state , with two cases. Either she sampled uniformly from with transition , in case of collision and if , or she sampled uniformly from with transition , if . In particular, note that if , transition is executed and not . Transition is a uniform sampling from (the “Musical Chair” step).
For player and round , we now introduce a few events that are useful in the proof. First, for every , we denote the event that a transition of type occurs for player after the first observations (i.e., between round and round , to decide ). Formally they are defined by
Then, we introduce as the event that a collision occurs for player at round if she is not yet fixed on her arm, that is
A key observation is that implies , as a collision necessarily involves at least one player not yet fixed on her arm (). Otherwise, if they are all fixed, i.e., for all , , then by definition of , none of the player changed their arm from to , and none experienced any collision at time so by induction there is no collision at time . Thus, can be upper bounded by (union bound), and it follows that if then
We can further observe that implies a transition or , as a transition cannot happen in case of collision. Thus another union bound gives
In the rest of the proof we focus on bounding the number of transitions and .
Let be the random variable denoting the number of transitions of type . Neglecting the event for and for , one has
which is (with known constants) by Lemma 5. In particular, this controls the second term in the right hand side of .
To control the first term we introduce three sequences of random variables, the starting times and the ending times (possibly larger than ), of sequences during which is true for all but not before and after, that is with the number of such sequences, i.e., (or if does not exist). If , the first sequence does not have term .
Now we can decompose the sum on with the use of consecutive sequences,
Both and have finite averages for any (as ), and is a stopping time with respect to the past events (that is, ), and so we can obtain
To control , we can observe that the number of sequences is smaller than plus the number of times when a sequence begins ( plus because maybe the game starts in a sequence). And beginning a sequence at time implies , which implies a transition of type or at time , as player j is in state “not fixed” at time (transitions and are impossible). As stated above, for both and , and so also.
To control , a simple argument can be used. implies for consecutive times. The very structure of gives that in this sequence of transitions , the successive collisions (i.e., ) implies that each new arm for is selected uniformly from , a set of size with at least one available arm. Indeed, as there is other players, at time at least one arm in is not selected by any player , and so player has at least a probability to select a free arm, which implies , and so implies the end of the sequence. In other words, the average length of sequences of transitions , , is bounded by the expected number of failed trial of a repeated Bernoulli experiment, with probability of success larger than (by the uniform choice of in a set of size with at least one available arm). We recognize the mean of a geometric random variable, of parameter , and so .
This finishes the proof as and so and finally also.
We can be more precise about the constants, all the previous arguments can be used successively:
And so we obtain the desired inequality, with explicit constants, that depend only on and .
Number of switches Note that we controlled the total number of transitions , and , which are the only transitions when a player can switch from arm to arm . Thus, the total number of arm switches is also proved to be logarithmic, if all players uses the - algorithm.
Strong uniform efficiency As soon as for all problem, is clearly proved to be uniformly efficient, as is for any . And as justified after Definition ? (page ), uniform efficiency and invariance under permutations of the users implies strong uniform efficiency, and so satisfies Definition ?. This is a sanity check: the lower-bound of Theorem 1 indeed applies to our algorithm , and finally this highlights that it is order-optimal for the regret, in the sense that it matches the lower-bound up-to a multiplicative constant, and optimal for the term (a).
EAdditionnal Discussions on
As said before, analyzing is harder, but for instance one can prove that it yields constant collisions and regret for the trivial case of and . Empirically, when is compared to the other algorithms, it is hard to find a case when performs badly, as its (empirical average) regret always appeared logarithmic. But an issue of only visualizing the empirical average regret for a certain number of repetitions is that if a certain “bad” run happens only with small probability, it is possible that it never happened in a simulation, or that it happened a few times but not enough to make the average regret look non-logarithmic
The intuition behind these configurations when performs poorly is the following, if all players use the same algorithm and the same indices. If two players and have exactly the same vectors and at some time step , with different values for each and so that the index vectors have different values for each arm , then both players will take the same decisions at time , and collide. Colliding does not change but increase one value in by . Then at the next step the same conditions on and are preserved, and if the same condition on are also preserved, the two players will continue to collide. We did not succeed in proving mathematically that the preservation of the first hypothesis on and implies the preservation of the hypothesis on index , but numerically it turns out to be always the case: and so two players colliding in such a setting will continue to do so infinitely: we denote such configurations as absorbing.
We wrote a script
![fig: Figure 6: For K=2 arms and M=2 players using \mathrm{Selfish}-\mathrm{UCB}_1, for depth=3: 2 absorbing configurations. Each rectangle represents a configuration, as the matrix [[\widetilde{S_k}^j(t) / T_k^j(t) ]_j]_k. Absorbing configurations from depth 2 are case of equality of the two vectors and the \mathrm{Selfish} indices \widetilde{g_k}^j(t). Transitions are labeled with their probabilities.](figures/Figure4_TikZ.png)
From the structure of such game tree, we conjecture that the probability of reaching absorbing configurations (before a certain time ) is always lower-bounded by a polynomial function of and , of degree at most in each variable. As such, the lower bound on probability of failures should decrease when and increase, and this is coherent with the experiments for or (see Figures Figure 14 and Figure 15), where is shown to be uniformly more efficient than . Of course, one cannot run an infinite number of simulations, and the smaller the probability of failure, the less likely it is to observe a failure in a finite number of runs.
Ideas to fix ? It could be possible to change the algorithm to add a way to escape such absorbing trajectories. For instance one could imagine that after seen seeing, e.g., collisions in a row, a certain random action could be taken by the players. These tricks can work empirically in some cases, but they are harder to analyze formally, and it is hard to tune the parameters (here , but possibly more), and we do not find such tricks to be promising from a theoretical point-of-view.
FAdditional Figures
The plots missing from Section 5 are included here, as well as some additional numerical results.
f.1Illustration of the lower bound
We proved in Theorem 1 that the normalized regret, i.e., divided by , is asymptotically lower bounded by a constant depending on the problem and the number of players , for any .
For an example problem with arms, we display below on the axis is the number of player, from player to players, and on the axis is the value of this constant , from the initial theorem and from our theorem. We chose a simple problem, with Bernoulli distributed arms, with . Figure 7 clearly shows that our improved lower bound is indeed larger than the initial one by [23], and both become uninformative when (i.e., null).
![fig: Figure 7: Comparison of our lower bound against the one from , on a simple problem with 9 Bernoulli arms, of means \boldsymbol{\mu} = [0.1, 0.2, \dots, 0.9], as a function of the number of players M.](figures/Comparison_of_our_lowerbound_and_Anandkumar_2010__9_arms.png)
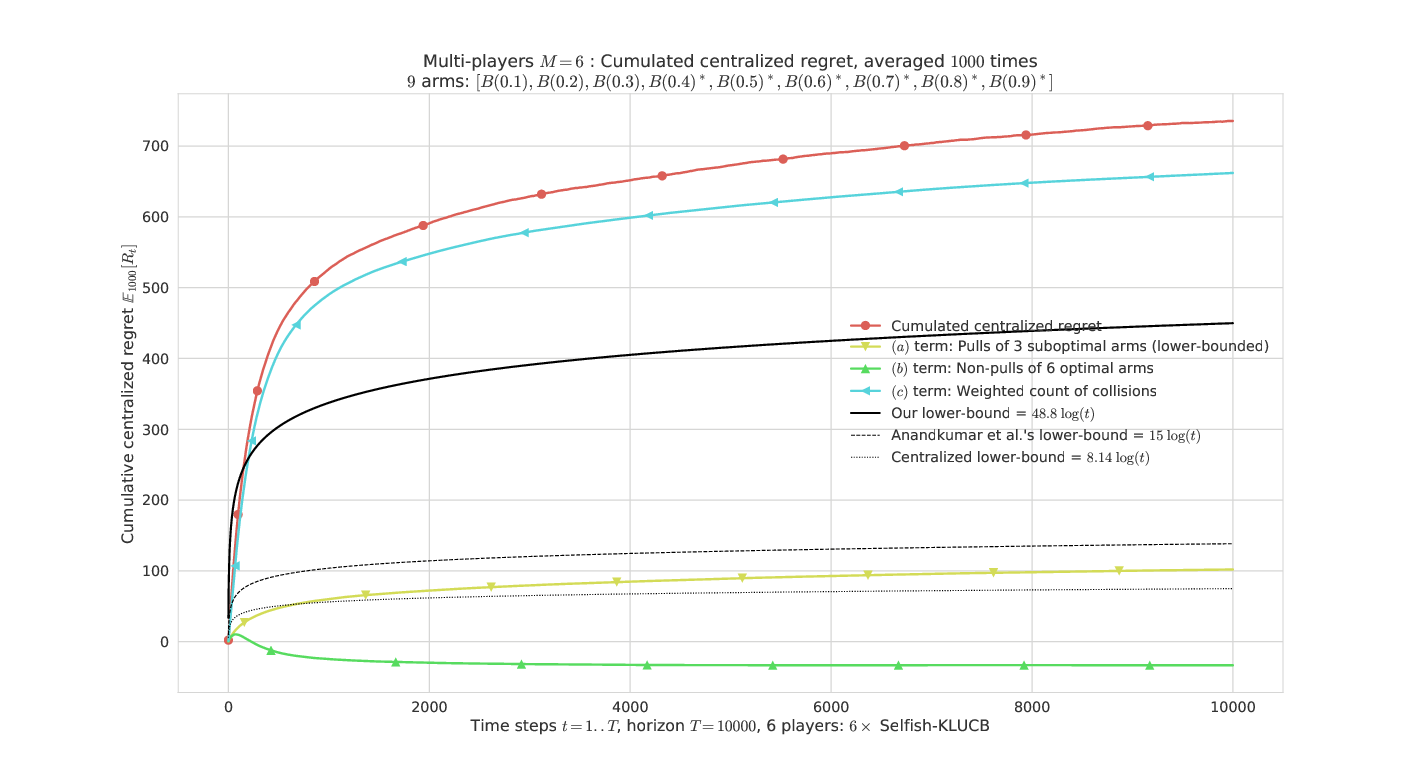
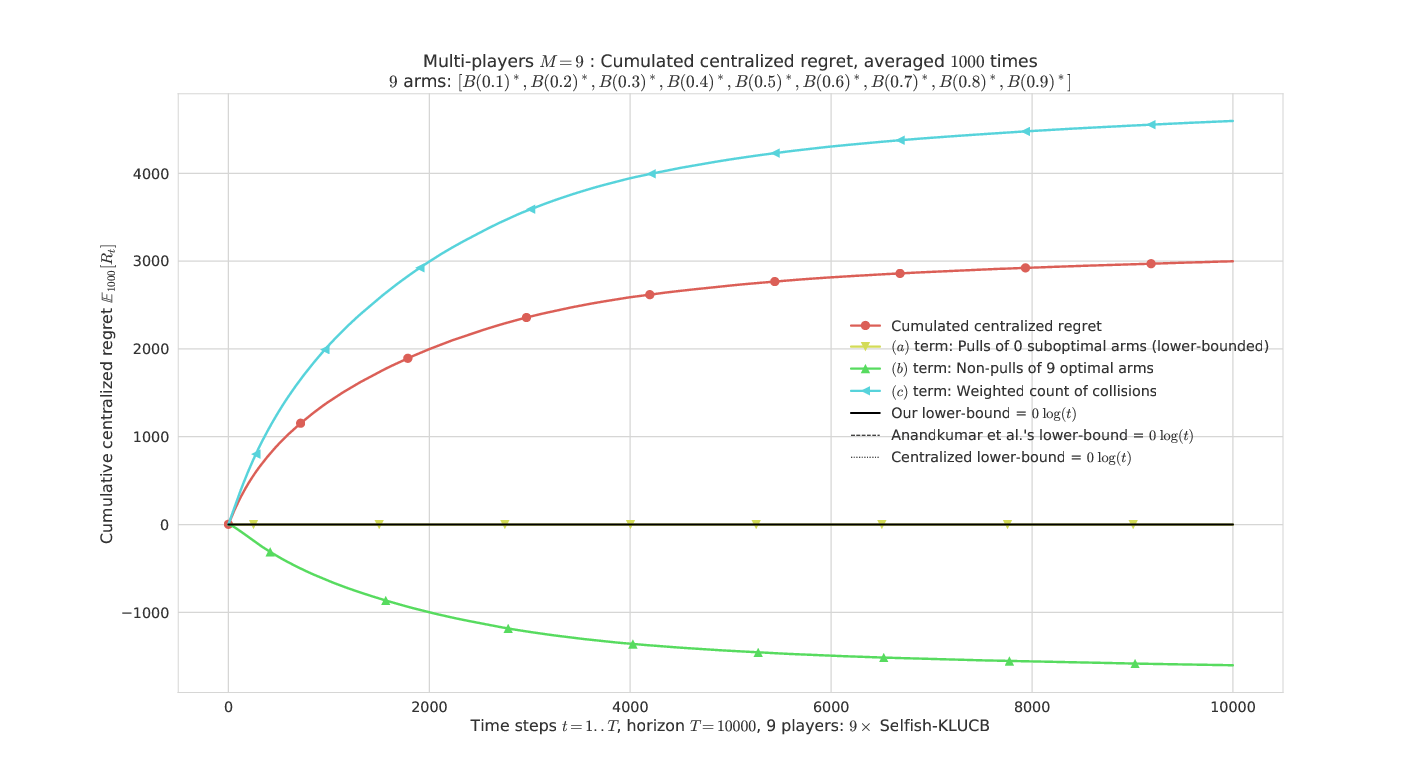
Figures Figure 8 show the regret on the same example problem , with arms and respectively , or players, for -. It is just a simple way to check that the two lower bounds on the regret indeed appear as valid lower bounds empirically, and are moreover lower bounds on the count of selections ((a), displayed in cyan). The lower bounds (in black) are , the dashed line for [23]’s lower bound, and the continuous line is our lower bound. These plot show the regret (in red), and the three terms (a), (b), (c) in the decomposition of the regret. As explained in Lemma 1, term (b) is not always non-negative. For and , (c) is actually larger than the regret, and term (a) is zero, as well as the lower bounds.
f.2Figures from Section
This last Appendix includes the figures used in Section 5, with additional comments.
![fig: Figure 9: Regret for M=2 players, K=3 arms, horizon T=5000, 1000 repetitions and \boldsymbol{\mu} = [0.1, 0.5, 0.9]. Axis x is for regret (different scale for each part), and the green curve for \mathrm{Selfish} shows a small probability of having a linear regret (17 cases of R_T \geq T, out of 1000). The regret for the three other algorithms is very small for this problem, always smaller than 100 here.](figures/MP__K3_M2_T5000_N1000__4_algos/all_HistogramsRegret____env1-1_5016720151160452442.png)
![fig: Figure 10: Regret, M=2 and M=3 players, K=3 arms, horizon T=5000, against 1000 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. \mathrm{Selfish} (top curve in green) clearly fails in such setting with small K.](figures/MP__K3_M2_T5000_N1000__4_algos/all_RegretCentralized____env1-1_2643560344649862285.png)
![fig: Regret, M=2 and M=3 players, K=3 arms, horizon T=5000, against 1000 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. \mathrm{Selfish} (top curve in green) clearly fails in such setting with small K.](figures/MP__K3_M3_T5000_N1000__4_algos/all_RegretCentralized____env1-1_4683123079851881812.png)
![fig: Figure 11: Regret for M=3 players, K=3 arms, horizon T=5000, 1000 repetitions and \boldsymbol{\mu} = [0.1, 0.5, 0.9]. Axis x is for regret (different scale for each), and the top green curve for \mathrm{Selfish} shows a small probability of having a linear regret (11 cases of R_T \geq T, out of 1000). The regret for the three other algorithms is very small for this problem, and even appears constant.](figures/MP__K3_M3_T5000_N1000__4_algos/all_RegretCentralized____env1-1_1035303196230283176.png)
![fig: Regret for M=3 players, K=3 arms, horizon T=5000, 1000 repetitions and \boldsymbol{\mu} = [0.1, 0.5, 0.9]. Axis x is for regret (different scale for each), and the top green curve for \mathrm{Selfish} shows a small probability of having a linear regret (11 cases of R_T \geq T, out of 1000). The regret for the three other algorithms is very small for this problem, and even appears constant.](figures/MP__K3_M3_T5000_N1000__4_algos/all_HistogramsRegret____env1-1_1035303196230283176.png)
![fig: Figure 12: Regret, M=2 players, K=9 arms, horizon T=5000, against 500 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. \mathrm{Rho}\mathrm{Rand} (top blue) is outperformed by the other algorithms (and the gain increases when M increases), which all perform similarly in such configurations. Note that the (small) tail of the histograms come from complicated problems \boldsymbol{\mu} and not failure cases.](figures/MP__K9_M2_T5000_N500__4_algos/all_RegretCentralized____env1-1_3251433209347345969.png)
![fig: Regret, M=2 players, K=9 arms, horizon T=5000, against 500 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. \mathrm{Rho}\mathrm{Rand} (top blue) is outperformed by the other algorithms (and the gain increases when M increases), which all perform similarly in such configurations. Note that the (small) tail of the histograms come from complicated problems \boldsymbol{\mu} and not failure cases.](figures/MP__K9_M2_T5000_N500__4_algos/all_HistogramsRegret____env1-1_3251433209347345969.png)
![fig: Figure 13: Regret, M=9 players for K=9 arms, horizon T=5000, against 500 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. This extreme case M=K shows the drastic difference of behavior between \mathrm{RandTopM} and \mathrm{MCTopM}, having constant regret, and \mathrm{Rho}\mathrm{Rand} and \mathrm{Selfish}, having large regret.](figures/MP__K9_M9_T5000_N500__4_algos/all_RegretCentralized____env1-1_3892966382091165662.png)
![fig: Regret, M=9 players for K=9 arms, horizon T=5000, against 500 problems \boldsymbol{\mu} uniformly sampled in [0,1]^K. This extreme case M=K shows the drastic difference of behavior between \mathrm{RandTopM} and \mathrm{MCTopM}, having constant regret, and \mathrm{Rho}\mathrm{Rand} and \mathrm{Selfish}, having large regret.](figures/MP__K9_M9_T5000_N500__4_algos/all_HistogramsRegret____env1-1_3892966382091165662.png)
![fig: Figure 14: Regret (in \log\log scale), for M=2 and 9 players for K=9 arms, horizon T=5000, for problem \boldsymbol{\mu}=[0.1,\dots,0.9]. In different settings, \mathrm{RandTopM} (yellow curve) and \mathrm{Selfish} (green) can outperform each other, and always outperform \mathrm{Rho}\mathrm{Rand}. \mathrm{MCTopM} is always among the best algorithms, and for M not too small, its regret seems logarithmic with a constant matching the lower bound.](figures/MP__K9_M2_T10000_N1000__4_algos/all_RegretCentralized_loglog____env1-1_2643359116089264295.png)
![fig: Regret (in \log\log scale), for M=2 and 9 players for K=9 arms, horizon T=5000, for problem \boldsymbol{\mu}=[0.1,\dots,0.9]. In different settings, \mathrm{RandTopM} (yellow curve) and \mathrm{Selfish} (green) can outperform each other, and always outperform \mathrm{Rho}\mathrm{Rand}. \mathrm{MCTopM} is always among the best algorithms, and for M not too small, its regret seems logarithmic with a constant matching the lower bound.](figures/MP__K9_M9_T10000_N200__4_algos/all_RegretCentralized_loglog____env1-1_2306423191427933958.png)
Note the simulation code used for the experiments is using Python 3. It is open-sourced at https://GitHub.com/SMPyBandits/SMPyBandits, and documented at https://smpybandits.github.io/.
Footnotes
- This provides another reason to focus on the Bernoulli model. It is the hardest model, in the sense that receiving a reward zero is not enough to detect collisions. For other models, the data streams are usually continuously distributed, with no mass at zero. Hence receiving directly gives .
- When players choose arm at time , this counts as collisions, not just one. So counts the total number of colliding players rather than the number of collision events. There is small abuse of notation when calling it a number of collisions.
- With some arguments used in the proof of Lemma 2 to circumvent the fact that (b) may be negative.
- The decentralized algorithms were also compared to a centralized multiple-play or , as defined by [5], essentially to check that the “price of decentralized learning” is not too large, as our lower bound proved.
- But of course the means are unknown to the algorithms, and their order is not important.
- Introducing switching costs, like it was done in previous works, e.g., [29], could be an interesting future work.
- For instance, , and draws from a uniform variable in for new ranks or arms.
- denotes the sigma-Algebra generated by the observations .
- In the work of [14], the statement is more general and the probability of an event is replaced by the expectation of any -measurable random variable bounded in .
- For instance, looks more like than so an event yielding linear regret with “small” probability cannot be observed from a plot showing the average regret.
- Available at
http://banditslilian.gforge.inria.fr/docs/complete_tree_exploration_for_MP_bandits.html
References
- Sample mean based index policies by regret for the Multi-Armed Bandit problem.
R. Agrawal. Advances in Applied Probability - Analysis of Thompson sampling for the Multi-Armed Bandit problem.
S. Agrawal and N. Goyal. In JMLR, Conference On Learning Theory, 2012. - Opportunistic Spectrum Access with multiple users: Learning under competition.
A. Anandkumar, N. Michael, and A. K. Tang. In IEEE INFOCOM, 2010. - Distributed algorithms for learning and cognitive medium access with logarithmic regret.
A. Anandkumar, N. Michael, A. K. Tang, and S. Agrawal. IEEE Journal on Selected Areas in Communications - Asymptotically efficient allocation rules for the Multi-Armed Bandit problem with multiple plays - Part I: IID rewards.
V. Anantharam, P. Varaiya, and J. Walrand. IEEE Transactions on Automatic Control - Finite-time Analysis of the Multi-armed Bandit Problem.
P. Auer, N. Cesa-Bianchi, and P. Fischer. Machine Learning - The Non-Stochastic Multi Armed Bandit Problem.
P. Auer, N. Cesa-Bianchi, Y. Freund, and R. Schapire. SIAM Journal of Computing - Learning to Coordinate Without Communication in Multi-User Multi-Armed Bandit Problems.
O. Avner and S. Mannor. arXiv preprint arXiv:1504.08167 - Multi-user lax communications: a Multi-Armed Bandit approach.
O. Avner and S. Mannor. In IEEE INFOCOM. IEEE, 2016. - Multi-Armed Bandit Learning in IoT Networks: Learning helps even in non-stationary settings.
R. Bonnefoi, L. Besson, C. Moy, E. Kaufmann, and J. Palicot. In 12th EAI Conference on Cognitive Radio Oriented Wireless Network and Communication, CROWNCOM Proceedings, 2017. - Regret Analysis of Stochastic and Non-Stochastic Multi-Armed Bandit Problems.
S. Bubeck, N. Cesa-Bianchi, et al. Foundations and Trends in Machine Learning - Kullback-Leibler upper confidence bounds for optimal sequential allocation.
O. Cappé, A. Garivier, O-A. Maillard, R. Munos, and G. Stoltz. Annals of Statistics - Simple and scalable response prediction for display advertising.
O. Chapelle, E. Manavoglu, and R. Rosales. Transactions on Intelligent Systems and Technology - Explore First, Exploit Next: The True Shape of Regret in Bandit Problems.
A. Garivier, P. Ménard, and G. Stoltz. arXiv preprint arXiv:1602.07182 - Multi-Armed Bandit based policies for Cognitive Radio’s decision making issues.
W. Jouini, D. Ernst, C. Moy, and J. Palicot. In International Conference Signals, Circuits and Systems. IEEE, 2009. - Upper Confidence Bound Based Decision Making Strategies and Dynamic Spectrum Access.
W. Jouini, D. Ernst, C. Moy, and J. Palicot. In IEEE International Conference on Communications, 2010. - Decentralized Learning for Multi-Player Multi-Armed Bandits.
D. Kalathil, N. Nayyar, and R. Jain. In IEEE Conference on Decision and Control, 2012. - On Bayesian Upper Confidence Bounds for Bandit Problems.
E. Kaufmann, O. Cappé, and A. Garivier. In AISTATS, pages 592–600, 2012a. - Thompson sampling: an asymptotically optimal finite-time analysis.
E. Kaufmann, N. Korda, and R. Munos. 2012b. - Optimal Regret Analysis of Thompson Sampling in Stochastic Multi-Armed Bandit Problem with Multiple Plays.
J. Komiyama, J. Honda, and H. Nakagawa. In International Conference on Machine Learning, volume 37, pages 1152–1161, 2015. - Asymptotically Efficient Adaptive Allocation Rules.
T. L. Lai and H. Robbins. Advances in Applied Mathematics - A contextual-bandit approach to personalized news article recommendation.
L. Li, W. Chu, J. Langford, and R. E. Schapire. In Proceedings of the 19th international conference on World Wide Web, pages 661–670. ACM, 2010. - Distributed learning in Multi-Armed Bandit with multiple players.
K. Liu and Q. Zhao. IEEE Transaction on Signal Processing - Cognitive Radio: making software radios more personal.
J. Mitola and G. Q. Maguire. IEEE Personal Communications - Some aspects of the sequential design of experiments.
H. Robbins. Bulletin of the American Mathematical Society - Multi-Player Bandits – A Musical Chairs Approach.
J. Rosenski, O. Shamir, and L. Szlak. In International Conference on Machine Learning, pages 155–163, 2016. - Online Learning in Decentralized Multi-User Spectrum Access with Synchronized Explorations.
C. Tekin and M. Liu. In IEEE Military Communications Conference, 2012. - On the Likelihood that One Unknown Probability Exceeds Another in View of the Evidence of Two Samples.
W. R. Thompson. Biometrika - Bandits with Movement Costs and Adaptive Pricing.
K. Tomer, L. Roi, and Y.Mansour. In 30th Annual Conference on Learning Theory (COLT), volume 65 of JMLR Workshop and Conference Proceedings, pages 1242–1268, 2017.