Index of /publis/slides/2018_04__Presentation_IEEE_WCNC

	Name	Last modified	Size	Description
	Parent Directory		-
	plots/	2021-03-04 16:23	-
	.gitignore	2021-03-04 16:23	7
	Makefile	2021-03-04 16:23	1.5K
	README.md	2021-03-04 16:23	8.8K
	preprocess_tex.sh	2021-03-04 16:23	119
	slides.md	2021-03-04 16:23	9.0K
	slides.pdf	2021-03-04 16:23	1.9M
	slides.pdfpc	2021-03-04 16:23	32
	slides.tex	2021-03-04 16:23	22K
	slides_169.pdf	2021-03-04 16:23	847K
	slides_169.pdfpc	2021-03-04 16:23	36
	slides_pandoc.md	2021-03-04 16:23	10K
	slides_pandoc.pdf	2021-03-04 16:23	936K
	slides_pandoc.pdfpc	2021-03-04 16:23	39

---

author: Lilian Besson *Advised by Christophe Moy Émilie Kaufmann title: Aggregation of MAB Learning Algorithms for OSA institute: PhD Student, Team SCEE, IETR, CentraleSupélec, Rennes & Team SequeL, CRIStAL, Inria, Lille date: IEEE WCNC - 16th April 2018

lang: english

IEEE WCNC: « Aggregation of Multi-Armed Bandits Learning Algorithms for Opportunistic Spectrum Access »

• Date 📅 : $16$th of April $2018$

• Who: Lilian Besson 👋 , PhD Student in France, co-advised by

Christophe Moy @ CentraleSupélec & IETR, Rennes	Émilie Kaufmann @ Inria, Lille

See our paper HAL.Inria.fr/hal-01705292

---

Introduction

• Cognitive Radio (CR) is known for being one of the possible solution to tackle the spectrum scarcity issue

• Opportunistic Spectrum Access (OSA) is a good model for CR problems in licensed bands

• Online learning strategies, mainly using multi-armed bandits (MAB) algorithms, were recently proved to be efficient [Jouini 2010]

• 💥 But there is many different MAB algorithms… which one should you choose in practice?

$\Longrightarrow$ we propose to use an online learning algorithm to also decide which algorithm to use, to be more robust and adaptive to unknown environments.

---

⏲ Outline

1. Opportunistic Spectrum Access
2. Multi-Armed Bandits
3. MAB algorithms
4. Aggregation of MAB algorithms
5. Illustration

Please 🙏

Ask questions at the end if you want!

---

1. Opportunistic Spectrum Access

• Spectrum scarcity is a well-known problem
• Different range of solutions…
• Cognitive Radio is one of them
• Opportunistic Spectrum Access is a kind of cognitive radio

---

Communication & interaction model

• 📱 Primary users are occupying $K$ radio channels
• ☎ Secondary users can sense and exploit free channels: want to explore the channels, and learn to exploit the best one
• Discrete time for everything $t\geq1,t\in\mathbb{N}$

---

2. Multi-Armed Bandits

Model

• Again $K \geq 2$ resources (e.g., channels), called arms
• Each time slot $t=1,\ldots,T$, you must choose one arm, denoted $A(t)\in{1,\ldots,K}$
• You receive some reward $r(t) \sim \nu_k$ when playing $k = A(t)$
• Goal: maximize your sum reward $\sum\limits_{t=1}^{T} r(t)$
• Hypothesis: rewards are stochastic, of mean $\mu_k$. E.g., Bernoulli

Why is it famous?

Simple but good model for exploration/exploitation dilemma.

---

3. MAB algorithms

• Main idea: index $I_k(t)$ to approximate the quality of each arm $k$
• First example: UCB algorithm
• Second example: Thompson Sampling

---

3.1 Multi-Armed Bandit algorithms

Often index based

• Keep index $I_k(t) \in \mathbb{R}$ for each arm $k=1,\ldots,K$
• Always play $A(t) = \arg\max I_k(t)$
• $I_k(t)$ should represent our belief of the quality of arm $k$ at time $t$

Example: "Follow the Leader"

• $Xk(t) := \sum\limits{s < t} r(s) \bold{1}(A(s)=k)$ sum reward from arm $k$
• $Nk(t) := \sum\limits{s < t} \bold{1}(A(s)=k)$ number of samples of arm $k$
• And use $I_k(t) = \hat{\mu}_k(t) := \frac{X_k(t)}{N_k(t)}$.

---

3.2 First example of algorithm
Upper Confidence Bounds algorithm (UCB)

• Instead of using $I_k(t) = \frac{X_k(t)}{N_k(t)}$, add an exploration term $$ I_k(t) = \frac{X_k(t)}{N_k(t)} + \sqrt{\frac{\alpha \log(t)}{2 N_k(t)}} $$

Parameter $\alpha$: tradeoff exploration vs exploitation

• Small $\alpha$: focus more on exploitation
• Large $\alpha$: focus more on exploration

💥 Problem: how to choose "the good $\alpha$" for a certain problem?

---

3.3 Second example of algorithm
Thompson sampling (TS)

• Choose an initial belief on $\mu_k$ (uniform) and a prior $p^t$ (e.g., a Beta prior on $[0,1]$)
• At each time, update the prior $p^{t+1}$ from $p^t$ using Bayes theorem
• And use $I_k(t) \sim p^t$ as random index

Example with Beta prior, for binary rewards

• $p^t = \mathrm{Beta}(1 + \text{nb successes}, 1 + \text{nb failures})$.
• Mean of $p^t$ $= \frac{1 + X_k(t)}{2 + N_k(t)} \simeq \hat{\mu}_k(t)$.

💥 How to choose "the good prior" for a certain problem?

---

4. Aggregation of MAB algorithms

Problem

• How to choose which algorithm to use?
• But also… Why commit to one only algorithm?

Solutions

• Offline benchmarks?
• Or online selections from a pool of algorithms?

$\hookrightarrow$ Aggregation?

Not a new idea, studied from the 90s in the ML community.

• Also use online learning to select the best algorithm!

---

4.1 Basic idea for online aggregation

If you have $\mathcal{A}_1,\ldots,\mathcal{A}_N$ different algorithms

• At time $t=0$, start with a uniform distribution $\pi^0$ on ${1,\ldots,N}$ (to represent the trust in each algorithm)
• At time $t$, choose $a^t \sim \pi^t$, then play with $\mathcal{A}_{a^t}$
• Compute next distribution $\pi^{t+1}$ from $\pi^t$:
  • increase $\pi^{t+1}{a^t}$ if choosing $\mathcal{A}{a^t}$ gave a good reward
  • or decrease it otherwise

Problems

1. How to increase $\pi^{t+1}_{a^t}$ ?
2. What information should we give to which algorithms?

---

4.2 Overview of the Exp4 aggregation algorithm

For rewards in $r(t) \in [-1,1]$.

• Use $\pi^t$ to choose randomly the algorithm to trust, $a^t \sim \pi^t$
• Play its decision, $A{\text{aggr}}(t) = A{a^t}(t)$, receive reward $r(t)$
• And give feedback of observed reward $r(t)$ only to this one
• Increase or decrease $\pi^t{a^t}$ using an exponential weight: $$ \pi^{t+1}{a^t} := \pi^{t}{a^t} \times \exp\left(\eta_t \times \frac{r(t)}{\pi^t{a^t}}\right).$$
• Renormalize $\pi^{t+1}$ to keep a distribution on ${1,\ldots,N}$
• Use a sequence of decreasing learning rate $\eta_t = \frac{\log(N)}{t \times K}$ (cooling scheme, $\eta_t \to 0$ for $t\to\infty$)

---

Use an unbiased estimate of the rewards

Using directly $r(t)$ to update trust probability yields a biased estimator

• So we use instead $\hat{r}(t) = r(t) / \pi^t_{a}$ if we trusted algorithm $\mathcal{A}_a$
• This way

$$\mathbb{E}[\hat{r}(t)] = \sum\limits{a=1}^N \mathbb{P}(a^t = a) \mathbb{E}[r(t) / \pi^t{a}]$$ $$= \mathbb{E}[r(t)] \sum\limits{a=1}^N \frac{\mathbb{P}(a^t = a)}{\pi^t{a}} = \mathbb{E}[r(t)] $$

---

4.3 Our Aggregator aggregation algorithm

Improves on Exp4 by the following ideas:

• First let each algorithm vote for its decision $A_1^t,\ldots,A_N^t$

• Choose arm $A{\text{aggr}}(t) \sim p_j^{t+1} := \sum\limits{a=1}^N \pi_a^t \mathbf{1}(A_a^t = j)$

• Update trust for each of the trusted algorithm, not only one (i.e., if $Aa^t = A{\text{aggr}}^t$) $\hookrightarrow$ faster convergence

• Give feedback of reward $r(t)$ to each algorithm! (and not only the one trusted at time $t$) $\hookrightarrow$ each algorithm have more data to learn from

---

5. Some illustrations

• Artificial simulations of stochastic bandit problems
• Bernoulli bandits but not only
• Pool of different algorithms (UCB, Thompson Sampling etc)
• Compared with other state-of-the-art algorithms for expert aggregation (Exp4, CORRAL, LearnExp)
• What is plotted it the regret for problem of means $\mu1,\ldots,\mu_K$ : $$ R_T^{\mu}(\mathcal{A}) = \max_k (T \mu_k) - \sum{t=1}^T \mathbb{E}[r(t)] $$
• Regret is known to be lower-bounded by $C(\mu) \log(T)$
• and upper-bounded by $C'(\mu) \log(T)$ for efficient algorithms

---

On a simple Bernoulli problem

---

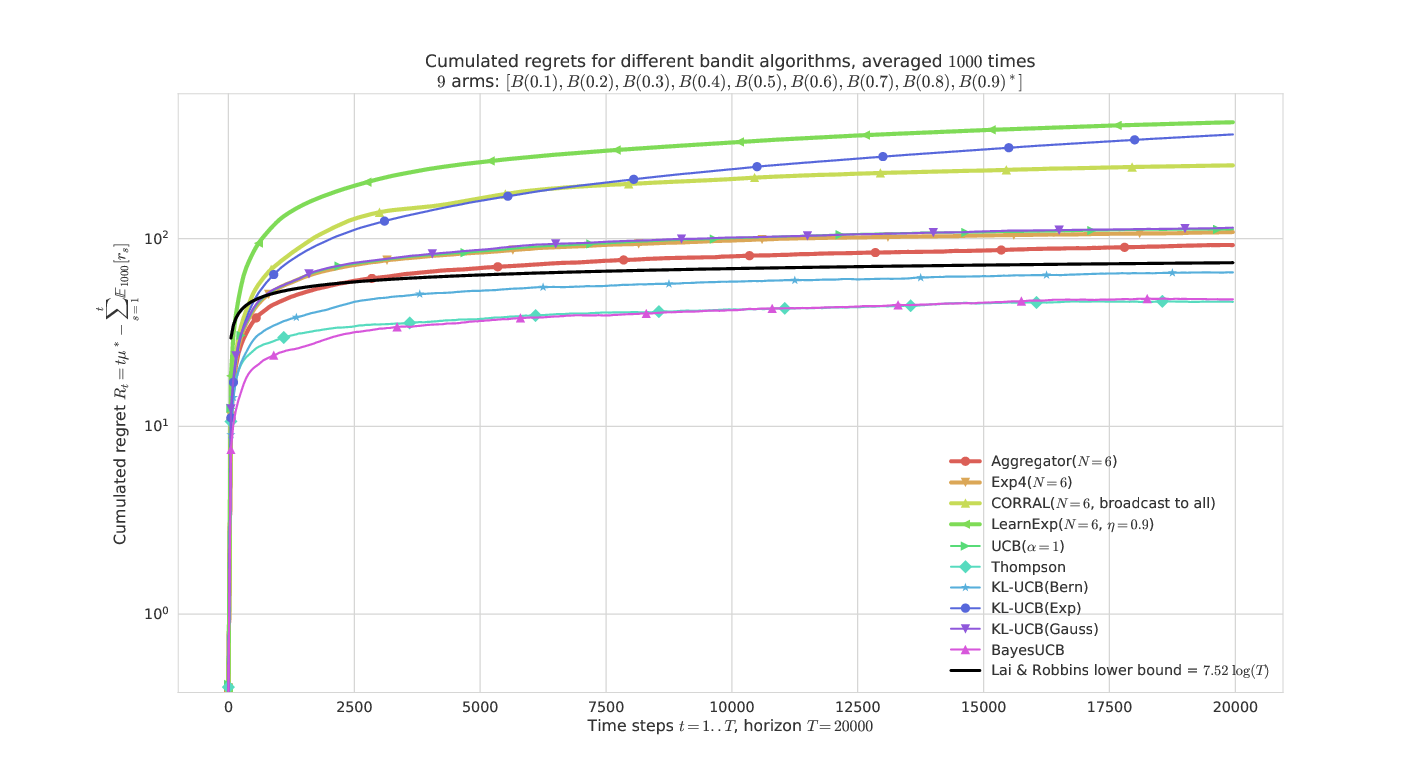
On a "hard" Bernoulli problem

---

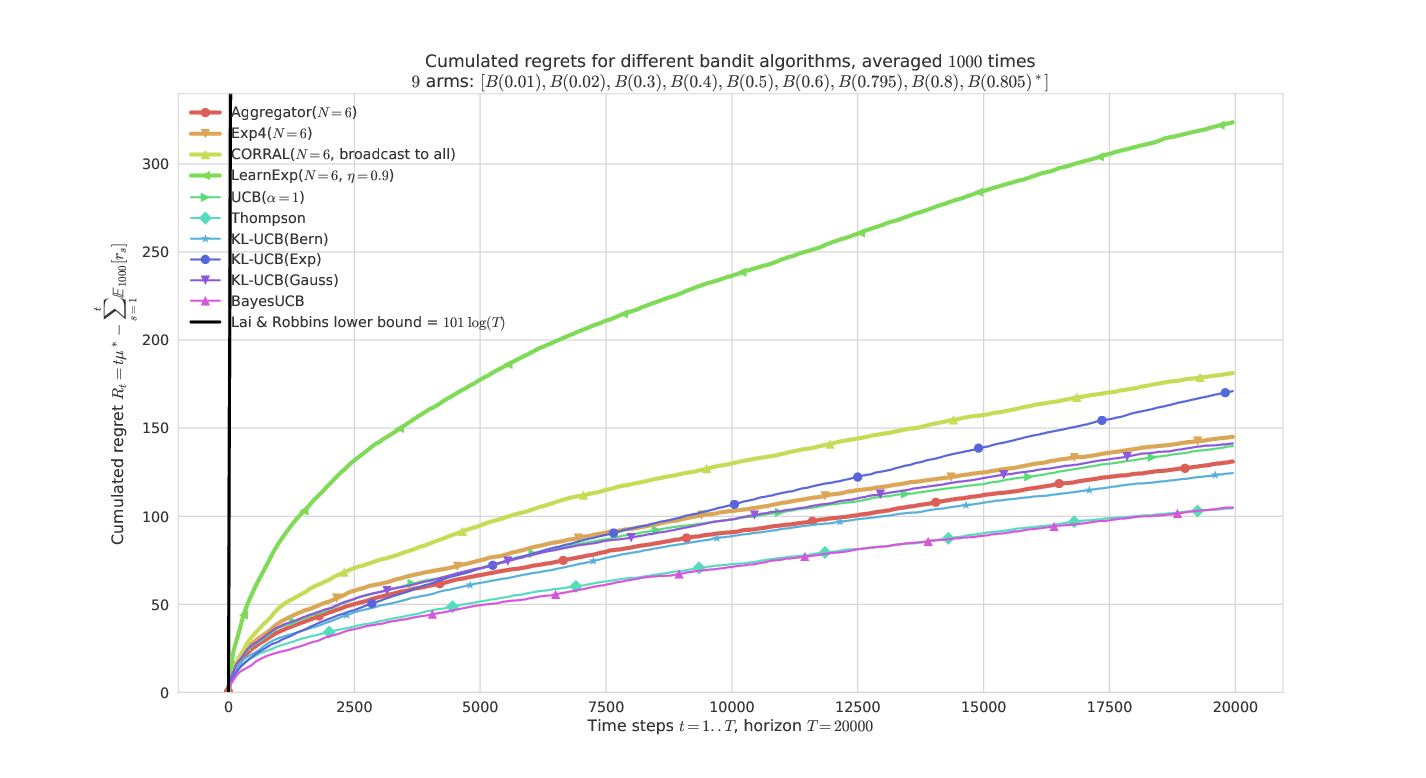
On a mixed problem

---

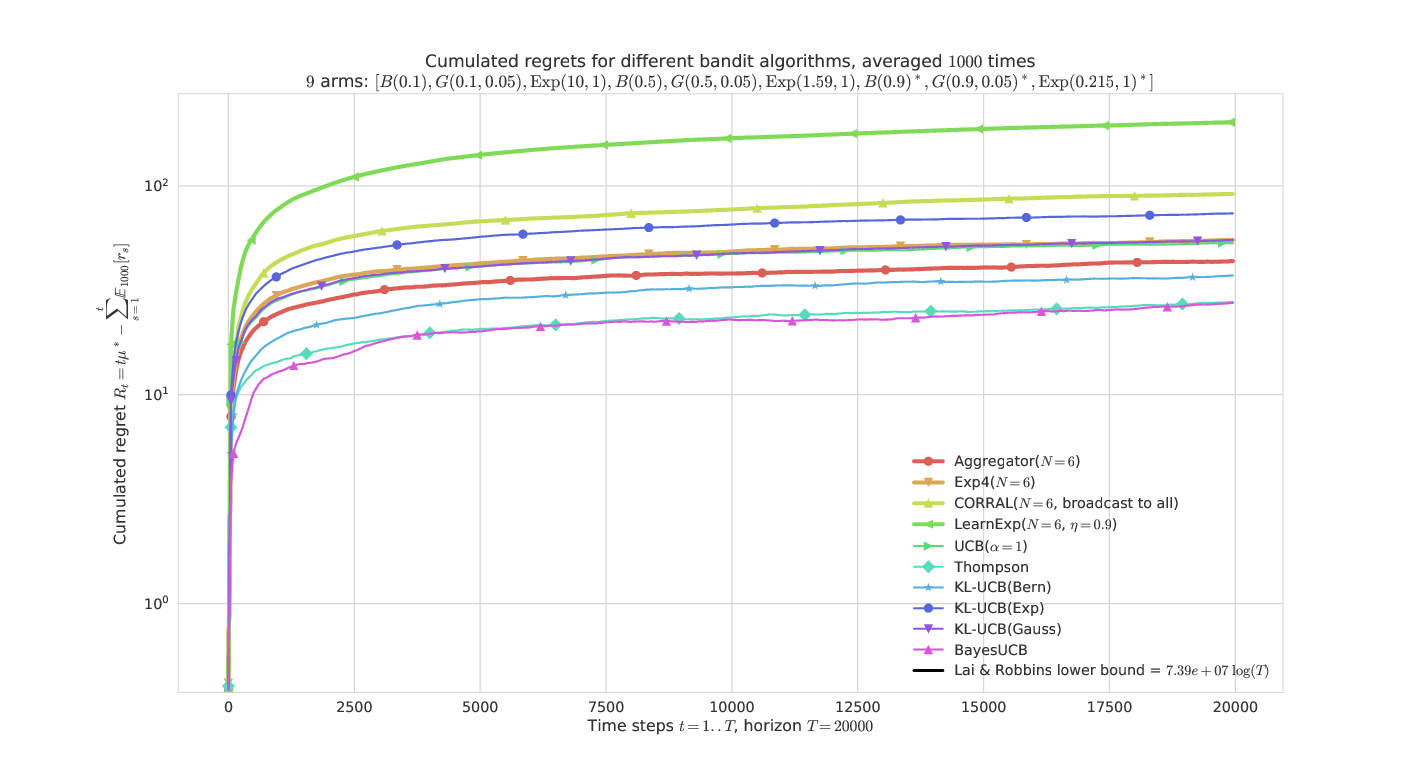
Conclusion (1/2)

• Online learning can be a powerful tool for Cognitive Radio, and many other real-world applications
• Many formulation exist, a simple one is the Multi-Armed Bandit
• Many algorithms exist, to tackle different situations
• It's hard to know before hand which algorithm is efficient for a certain problem…
• Online learning can also be used to select on the run which algorithm to prefer, for a specific situation!

---

Conclusion (2/2)

• Our algorithm Aggregator is efficient and easy to implement
• For $N$ algorithms $\mathcal{A}_1,\ldots,\mathcal{A}_N$, it costs $\mathcal{O}(N)$ memory, and $\mathcal{O}(N)$ extra computation time at each time step
• For stochastic bandit problem, it outperforms empirically the other state-of-the-arts (Exp4, CORRAL, LearnExp).

See our paper

HAL.Inria.fr/hal-01705292

See our code for experimenting with bandit algorithms

Python library, open source at SMPyBandits.GitHub.io

Thanks for listening !